【题目】某公司准备销售甲、乙两种材料中的一种，设年销售量为（单位：吨）（），若销售甲种材料，每吨成本为10万元，每吨售价（单位：万元）与的函数关系是：，设年利润为（单位：万元）（年利润＝销售额－成本）；若销售乙种材料，销售利润与的函数关系是：，同时每吨可获返利万元（），设年利润为（单位：万元）（年利润＝销售利润＋返利）．

（1）当时，________；

（2）当，时，________；

（3）求与的函数关系式，并求出为何值时，最大，最大值是多少？

【题目】某公司采用两种方式经营商品的销售业务，方式一：将商品精包装后直接销售；方式二：将商品深加工得到商品后再销售．已知商品的基础成本（万元）和精包装费用（万元）均与销售数量（吨）成正比，平均销售价格（万元/吨）与符合关系式，生产商品总费用（万元）包括每月固定环保费（万元）和每吨固定加工费（万元），其平均销售价格为9万元/吨．2月份该公司销售两种商品共20吨，销售利润60万元；3月份受季节影响，虽然也销售了20吨两种商品，但销售利润只有38万元，两个月的部分销售情况如下表．（销售利润＝销售总收入－经营总成本）

（1）当时，求商品的销售利润与之间的函数关系式；

（2）求出、的值；

（3）4月份该公司仍旧计划销售20吨两种商品，问：该公司能获得30万元销售利润吗？若能，请求出的值；若不能，请说明理由．

（1）请直接写出a的值为　 　；

（2）从第21天到第40天中，求q与x满足的关系式；

（3）若该网店第x天获得的利润y元，并且已知这40天里前20天中y与x的函数关系式为y＝﹣x2+15x+500

i请直接写出这40天中p与x的关系式为：　 　；

ii求这40天里该网店第几天获得的利润最大？

【题目】如图，足球场上守门员在处开出一高球，球从离地面1米的处飞出（在轴上），运动员乙在距点6米的处发现球在自己头的正上方达到最高点，距地面约4米高，球落地后又一次弹起．据实验测算，足球在草坪上弹起后的抛物线与原来的抛物线形状相同，最大高度减少到原来最大高度的一半．

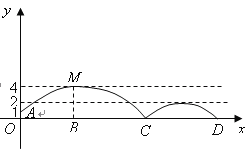
（1）求足球开始飞出到第一次落地时，该抛物线的表达式．

（2）足球第一次落地点距守门员多少米？（取）

（3）运动员乙要抢到第二个落点，他应再向前跑多少米？

（取）

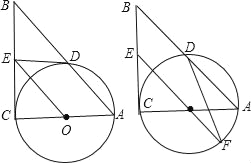
【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．

（1）求证：ED为⊙O的切线；

（2）如果⊙O的半径为，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．

【答案】（1）证明见解析；（2）

【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得≌ 即可得，则可证得为的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得 利用勾股定理即可求得的长，又由OE∥AB，证得根据相似三角形的对应边成比例，即可求得的长，然后利用三角函数的知识，求得与的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．

试题解析：(1)证明：连接OD，

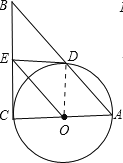
∵OE∥AB，

∴∠COE=∠CAD，∠EOD=∠ODA，

∵OA=OD,

∴∠OAD=∠ODA，

∴∠COE=∠DOE，

在△COE和△DOE中，

∴△COE≌△DOE(SAS)，

∴ED⊥OD，

∴ED是的切线；

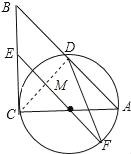
(2)连接CD，交OE于M，

在Rt△ODE中，

∵OD=32，DE=2，

∵OE∥AB，

∴△COE∽△CAB，

∴AB=5，

∵AC是直径，

∵EF∥AB，

∴S△ADF=S梯形ABEFS梯形DBEF

∴△ADF的面积为

【题型】解答题
【结束】
23

（1）二次函数和反比例函数的关系式．

（2）弹珠在轨道上行驶的最大速度．

【题目】某垃圾处理厂，只能处理、两类垃圾，且每天只能处理其中的一类垃圾，已知该垃圾厂每月工作25天，每天处理垃圾种类的吨数及费用如下表：

设该垃圾厂每月处理类垃圾天，这个厂每月处理垃圾的总吨数为吨，每月处理垃圾所需的总费用为元，据测算该厂每月最多处理垃圾590吨．

（1）求与的函数关系式；

（2）为何值时，最小，最小值是多少？

（3）一段时间后，由于改进了处理类垃圾的流程，使处理每吨类垃圾的费用减少了元（），类垃圾的处理费用没有改变，求该厂每月处理垃圾费用最少时，处理、两类垃圾的天数各是多少？

（1）小明和小华都在此驾校参加C2驾驶证的培训，下表是小明和小华的培训结算表（培训学时均为40），请你根据提供的信息，计算出a，b的值．

（2）小陈报名参加了C2驾驶证的培训，并且计划学够全部基本学时，但为了不耽误工作，普通时段的培训学时不会超过其他两个时段总学时的，若小陈普通时段培训了x学时，培训总费用为y元

①求y与x之间的函数关系式，并确定自变量x的取值范围；

②小陈如何选择培训时段，才能使得本次培训的总费用最低？

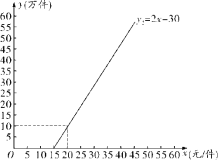
【题目】某地一种商品的需求量（万件）与商品价格（元/件）存在一次函数关系，且价格为10元/件时，需求量是50万件；当价格是20元/件时，需求量是40万件，该商品的供应量（万件）与商品的价格（元/件）的函数关系如图所示．

（1）求关于的函数关系式，并在坐标系中画出它的图象；

（2）要使商品价格相对稳定，需保持供应量与需求量的大致平衡（简称供需平衡），你认为商品的价格定在每件多少元时，供需最平衡；商品价格是每件多少元时，供大于求？

（3）当市场供应量大于需求量的时，政府就会发出预警，那么政府发出预警时，商品的最低价格是每件多少元？（精确到元）

樱桃单价w与上市时间x的关系

请解答下列问题：

（1）观察图象，直接写出日销售量的最大值；

（2）求小明家樱桃的日销售量y与上市时间x的函数解析式；

（3）求a的值；

（4）第12天的销售金额是最多的吗？请说明你的观点和依据．