
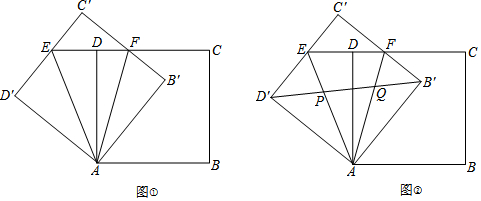
分析 (1)首先证明Rt△AD'E≌Rt△ADE(HL),推出D'E=DE,∠D'AE=∠DAE,同理:B'F=DF,∠B'AF=∠DAF,推出∠EAF=∠DAE+∠DAF=$\frac{1}{2}$∠B'AD'=45°,推出△EC′F的周长为C'E+EF+C'F=C'E+DE+DF+C'F=C'E+D'E+B'F+C'F=C'D+B'C'=2.
(2)求出B′D′的长即可解决问题.
(3)首先证明△APQ∽△AFE,推出$\frac{EF}{PQ}$=$\sqrt{2}$,推出EF最小时,△AEF的面积最小,此时△APQ的面积最小,由(1)可知,△C′EF的周长=EC′+C′F+EF=C′E+ED′+FB′=C′D′+C′B′=2=定值,可以证明当EC′=C′F时,斜边EF定值最小.求出△AEF的最小值即可解决问题.
解答 解:(1)∵正方形ABCD绕点A逆时针旋转α°,后得到正方形AB′C′D′,
∴∠D'AB'=∠D'=∠ADE=90°,AD'=AD=C'D'=B'C'=1
在Rt△AD'E和Rt△ADE中,
$\left\{\begin{array}{l}{AD′=AD}\\{AE=AE}\end{array}\right.$,
∴Rt△AD'E≌Rt△ADE(HL),
∴D'E=DE,∠D'AE=∠DAE,
同理:B'F=DF,∠B'AF=∠DAF,
∴∠EAF=∠DAE+∠DAF=$\frac{1}{2}$∠B'AD'=45°,
△EC′F的周长为C'E+EF+C'F=C'E+DE+DF+C'F=C'E+D'E+B'F+C'F=C'D+B'C'=2,
故答案为:45°,2;
(2)∵B'D'是正方形AB'C'D'的对角线,
∴B'D'=$\sqrt{2}$,
∵D′P=a,QB′=b
∴PQ=B'D'-D'P-B'Q=$\sqrt{2}$-a-b;
(3)如图②中,连接EQ.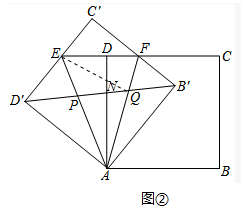
∵∠ED′P=∠PAQ=45°,∠EPD′=∠APQ,
∴△EPD′∽△QPA,
∴$\frac{EP}{PQ}$=$\frac{PD′}{AP}$,
∴$\frac{EP}{PD′}$=$\frac{PQ}{AP}$,∵∠APD′=∠EPQ,
∴△PAD′∽△PQE,
∴∠AD′P=∠PEQ=45°,
∴∠QAE=∠QEA=45°,
∴△AEQ是等腰直角三角形,
∴AE=$\sqrt{2}$AQ,同理,AF=$\sqrt{2}$AP,
∴$\frac{AP}{AF}$=$\frac{AQ}{AE}$,∵∠PAQ=∠EAF,
∴△PAQ∽△FAE,
∴$\frac{EF}{PQ}$=$\sqrt{2}$,
∵EF最小时,△AEF的面积最小,此时△APQ的面积最小,
由(1)可知,△C′EF的周长=EC′+C′F+EF=C′E+ED′+FB′=C′D′+C′B′=2=定值,
可以证明当EC′=C′F时,斜边EF定值最小.设C′E=x,C′F=y,EF=z,则x+y+z=2,x2+y2=z2,x+y=2-z,xy=2-2z,
∴x,y是方程M的两根,M2-(2-z)M+2-2z=0,∵△≥0,
∴(2-z)2-4(2-2z)≥0,
∴(z+2)2≥8,
∴z+2≥2$\sqrt{2}$,
∴z$≥2\sqrt{2}$-2,
∴斜边EF的最小值为2$\sqrt{2}$-2,此时△AEF的面积=$\frac{1}{2}$×1×(2$\sqrt{2}$-2)=$\sqrt{2}$-1,△APQ的面积=$\frac{1}{2}$•S△AEF=$\frac{\sqrt{2}-1}{2}$,
∴△APQ的面积的最小值为$\frac{\sqrt{2}-1}{2}$.
点评 本题考查正方形的性质、全等三角形的判定和性质、相似三角形的判定和性质、等腰直角三角形的判定和性质、勾股定理、一元二次方程的根的判别式等知识,解题的关键是灵活运用所学知识解决问题,本题的难点是构建一元二次方程,应用故的判别式,确定EF的最小值,属于中考压轴题.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
 如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.
如图,在边长为3的正方形ABCD中,点E是BC边上的点,BE=1,∠AEP=90°,且EP交正方形外角的平分线CP于点P,交边CD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,-1) | B. | (2,-1) | C. | (1,-2) | D. | (2,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16℃ | B. | -16℃ | C. | 20℃ | D. | -20℃ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
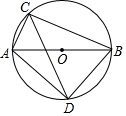 如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.
如图,AB是⊙O的直径,弦BC长为$4\sqrt{2}$,弦AC长为2,∠ACB的平分线交⊙O于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com