
【题目】某学校为了开展“阳光体育运动”,计划购买篮球与足球共![]() 个,已知每个篮球的价格为
个,已知每个篮球的价格为![]() 元,每个足球的价格为
元,每个足球的价格为![]() 元
元
(1)若购买这两类球的总金额为![]() 元,求篮球和足球各购买了多少个?
元,求篮球和足球各购买了多少个?
(2)元旦期间,商家给出蓝球打九折,足球打八五折的优惠价,若购买这种篮球与足球各![]() 个,那么购买这两类球一共需要多少钱?
个,那么购买这两类球一共需要多少钱?
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD、DEFG都是正方形,连接AE、CG.

(1)求证:AE=CG;
(2)观察图形,猜想AE与CG之间的位置关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
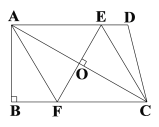
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠B=90°,对角线AC的垂直平分线与边AD、BC分别相交于点E、F.
(1)求证:四边形AFCE是菱形;
(2)若AB=6,BC=8,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
某校要举办足球赛,若有5支球队进行单循环比赛(即全部比赛过程中任何一队都要分别与其他各队比赛一场且只比赛一场),则该校一共要安排多少场比赛?
构建模型:
生活中的许多实际问题,往往需要构建相应的数学模型,利用模型的思想来解决问题.
为解决上述问题,我们构建如下数学模型:
(1)如图①,我们可以在平面内画出5个点(任意3个点都不在同一条直线上),其中每个点各代表一支足球队,两支球队之间比赛一场就用一条线段把他们连接起来.由于每支球队都要与其他各队比赛一场,即每个点与另外4个点都可连成一条线段,这样一共连成5×4条线段,而每两个点之间的线段都重复计算了一次,实际只有 条线段,所以该校一共要安排 场比赛.

(2)若学校有6支足球队进行单循环比赛,借助图②,我们可知该校一共要安排__________场比赛;
…………
(3)根据以上规律,若学校有n支足球队进行单循环比赛,则该校一共要安排___________场比赛.
实际应用:
(4)9月1日开学时,老师为了让全班新同学互相认识,请班上42位新同学每两个人都相互握一次手,全班同学总共握手________________次.
拓展提高:
(5)往返于青岛和济南的同一辆高速列车,中途经青岛北站、潍坊、青州、淄博4个车站(每种车票票面都印有上车站名称与下车站名称),那么在这段线路上往返行车,要准备车票的种数为__________种.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
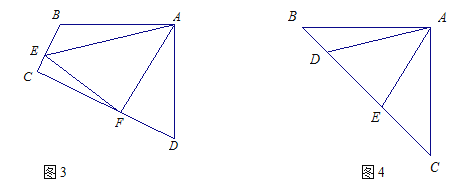
小炎遇到这样一个问题:如图1,点E、F分别在正方形ABCD的边BC,CD上,∠EAF=45°,连结EF,则EF=BE+DF,试说明理由.

小炎是这样思考的:要想解决这个问题,首先应想办法将这些分散的线段相对集中.她先后尝试了翻折、旋转、平移的方法,最后发现线段AB,AD是共点并且相等的,于是找到解决问题的方法.她的方法是将△ABE绕着点A逆时针旋转90°得到△ADG,再利用全等的知识解决了这个问题(如图2).
参考小炎同学思考问题的方法,解决下列问题:
(1)如图3,四边形ABCD中,AB=AD,∠BAD=90°点E,F分别在边BC,CD上,∠EAF=45°.若∠B,∠D都不是直角,则当∠B与∠D满足_ 关系时,仍有EF=BE+DF;
(2)如图4,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°,若BD=1, EC=2,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“书香校园”号召,重庆一中在九年级学生中随机抽取某班学生对2016年全年阅读中外名著的情况进行调查,整理调查结果发现,每名学生阅读中外名著的本数,最少的有5本,最多的有8本,并根据调查结果绘制了如图所示的不完整的折线统计图和扇形统计图.

(1)该班学生共有 名,扇形统计图中阅读中外名著本数为7本所对应的扇形圆心角的度数是 度,并补全折线统计图;
(2)根据调查情况,班主任决定在阅读中外名著本数为5本和8本的学生中任选两名学生进行交流,请用树状图或表格求出这两名学生阅读的本数均为8本的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
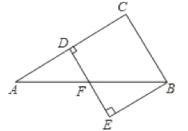
【题目】如图.△ABC中,AC的垂直平分线分别交AC、AB于点D. F,BE⊥DF交DF的延长线于点E,已知∠A=30°,BC=2,AF=BF,则四边形BCDE的面积是_____
查看答案和解析>>
科目:初中数学 来源: 题型:
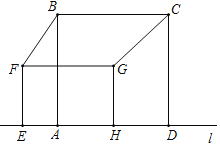
【题目】如图,正方形ABCD与矩形EFGH在直线l的同侧,边AD,EH在直线l上,且AD=5cm,EH=4cm,EF=3cm.保持正方形ABCD不动,将矩形EFGH沿直线l左右移动,连接BF,CG,则BF+CG的最小值为_____________cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com