
【题目】如图,在矩形ABCD中,BC=8,AB=6,经过点B和点D的两个动圆均与AC相切,且与AB、BC、AD、DC分别交于点G、H、E、F,则EF+GH的最小值是( )
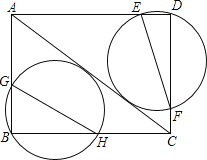
A.6 B.8 C.9.6 D.10
【答案】C
【解析】
试题分析:如图,设GH的中点为O,过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,根据∠B=90°可知,点O为过B点的圆的圆心,OM为⊙O的半径,BO+OM为直径,可知BO+OM≥BN,故当BN为直径时,直径的值最小,即直径GH也最小,同理可得EF的最小值.
解:如图,设GH的中点为O,
过O点作OM⊥AC,过B点作BN⊥AC,垂足分别为M、N,
在Rt△ABC中,BC=8,AB=6,
∴AC=![]() =10,
=10,
由面积法可知,BN![]() AC=AB
AC=AB![]() BC,
BC,
解得BN=4.8,
∵∠B=90°,
∴GH为⊙O的直径,点O为过B点的圆的圆心,
∵⊙O与AC相切,
∴OM为⊙O的半径,
∴BO+OM为直径,
又∵BO+OM≥BN,
∴当BN为直径时,直径的值最小,
此时,直径GH=BN=4.8,
同理可得:EF的最小值为4.8,
∴EF+GH的最小值是9.6.
故选C.



 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
【题目】手工课上,老师将同学们分成A,B两个小组制作两个汽车模型,每个模型先由A组同学完成打磨工作,再由B组同学进行组装完成制作,两个模型每道工序所需时间如下:

则这两个模型都制作完成所需的最短时间为( )
A. 20分钟 B. 22分钟 C. 26分钟 D. 31分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在操场上做游戏,他发现地上有一个不规则的封闭图形ABC.为了知道它的面积,他在封闭图形内划出了一个半径为1米的圆,在不远处向图形内掷石子,且记录如下:

(1)随着次数的增多,小明发现m与n的比值在一个常数k附近波动,请你写出k的值。
(2)请利用学过的知识求出封闭图形ABC的大致面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A与点B关于x轴对称,点A的坐标为(﹣1,2),则点B的坐标是( )
A. (﹣1,2) B. (﹣1.﹣2) C. (1,2) D. (﹣2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CA⊥AB,垂足为点A,AB=24,AC=12,射线BM⊥AB,垂足为点B,一动点E从A点出发以3厘米/秒沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E经过秒时,△DEB与△BCA全等. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°. 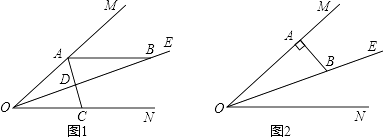
(1)如图1,若AB∥ON,则
①∠ABO的度数是;
②当∠BAD=∠ABD时,x=;当∠BAD=∠BDA时,x= .
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,以下结论:①∠BAC=70°;②∠DOC=90°;③∠BDC=35°;④∠DAC=55°,其中正确的是 . (填写序号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
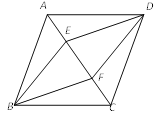
【题目】如图,在四边形ABCD中,AB∥CD,点E、F在对角线AC上,且∠ABF=∠CDE,AE=CF.
(1)求证:△ABF≌△CDE;
(2)当四边形ABCD满足什么条件时,四边形BFDE是菱形?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com