
分析 (1)分k=0和k≠0两种情况讨论,若k≠0,只要让根的判别式△=b2-4ac≥0且k≠0,求得k的取值即可;
(2)只要让根的判别式△=b2-4ac=0,求得k的值,进而求得方程的解即可.
解答 解:(1)当k=0时,x=$\frac{3}{2}$,满足题意,
当k≠0时,由题意得:36-36k≥0且k≠0,
解得:k≤1且k≠0;
综上k的取值范围是k≤1;
(2)由题意得:36-36k=0,
解得:k=1,
∴原方程化为:x2-6x+9=0,
解得:x1=x2=3.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
 如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:
如图,点A,B,C在同一条直线上,△ABD,△BCE均为等边三角形,连接AE和CD,AE分别交CD、BD于点M、P,CD交BE于点Q,连接PQ,BMM、P,CD交BE于点Q,连接PQ,BM,下面结论:| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个. |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
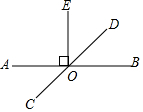 如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )
如图,直线AB与CD相交于点O,若∠AOC=$\frac{1}{3}$∠AOD,则∠BOD的度数为( )| A. | 30° | B. | 45° | C. | 60° | D. | 135° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
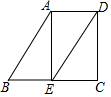 如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.
如图,已知AB∥DE,∠B=60°,AE⊥BC,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a5+a5=2a10 | B. | ${a^{-2}}•{a^{-3}}=\frac{1}{a^6}$ | C. | [(-a)3]2=(-a)6=a6 | D. | a5÷a5=a5-5=a0=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
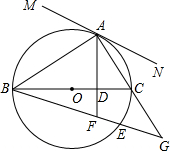 如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G.
如图,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D,$\underset{\widehat{AB}}{\;}$=$\widehat{AE}$,BE分别交AD、AC延长线于点F、G.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com