
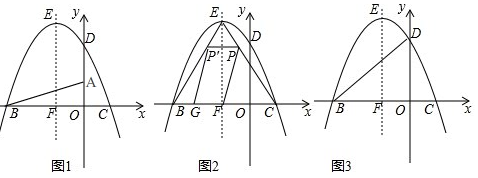
���� ��1���������C��D��B�����꣬���ô���ϵ������������߽���ʽ��д�ɶ���ʽ���������E���ꣻ
��2�������CB��EF�����жϳ���EPP'�ס�ECB�ó�����ʽ�ó�HF���ɵó�y��x�ĺ�����ϵʽ�������y�����ֵ��
��3�������OM�Ľ���ʽ������������١�BDQ=90��͢ڡ�DBQ=90����ֱ�ߺ������ߵĽ���ʽ���������������Q�����꣮
��� �⣺��1������ת֪����COD�ա�AOB��
��OC=OA��OD=OB��
��OC=2��OD=4��
��C��2��0����D��0��4����B��-4��0����
���������ߵĽ���ʽΪy=a��x-2����x+4����
�ѵ�D��0��4�����������߽���ʽ�У��ó�a=-$\frac{1}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$��x-2����x+4��=-$\frac{1}{2}$��x+1��2+$\frac{9}{2}$��
��E��-1��$\frac{9}{2}$����
��2����PP'��EF��H��
��PP'��BC��PE��P'G��
���ı���FGP'P��ƽ���ı��Σ�
��PP'=FG��
���EPP'�ס�ECB��
��$\frac{PP'}{CB}=\frac{EH}{EF}=\frac{EF-HF}{EF}$��
��C��2��0����B��-4��0����E��-1��$\frac{9}{2}$����
��FG=x����CB=6��EF=$\frac{9}{2}$��PP'=x��
��$\frac{x}{6}=\frac{\frac{9}{2}-HF}{\frac{9}{2}}$��
��HF=$\frac{9}{2}-\frac{3}{4}x$��
��S�ı���FPP��G=FG•FH��
��y=x��$\frac{9}{2}-\frac{3}{4}x$��=-$\frac{3}{4}$��x-3��2+$\frac{27}{4}$��
�൱x=3ʱ��y�����ֵΪ$\frac{27}{4}$��
��3������������������ĵ�Q��x��y������OM��BD��M��
��BD��Rt��BDQ��ֱ�DZߣ�
��Rt��BDQ����һֱ�DZ���OMƽ�У�
��OD=OB��OD��OB��OB=4��OC=4��
��Rt��BCQ����һֱ�DZ����ڵ�ֱ�߿�����ֱ��OM���ϻ�����ƽ��4����λ�õ���
��ͼ��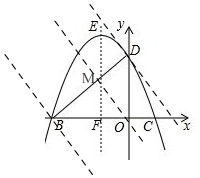 ��ֱ��OM�Ľ���ʽΪy=x��
��ֱ��OM�Ľ���ʽΪy=x��
��Rt��BDQ����һֱ�DZ����ڵ�ֱ�߽���ʽΪy=-x+4��y=-x-4��
�ٵ�QΪֱ��y=-x+4�������ߵĽ��㣬
��$\left\{\begin{array}{l}{y=-x+4}\\{y=-\frac{1}{2}��x+1��^{2}+\frac{9}{2}}\end{array}\right.$��
��$\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$����ʱ��Q�͵�D�غϣ����������⣬��ȥ��
�ڵ�QΪֱ��y=-x-4�������ߵĽ��㣬
��$\left\{\begin{array}{l}{y=-x-4}\\{y=-\frac{1}{2}��x+1��^{2}+\frac{9}{2}}\end{array}\right.$��
��$\left\{\begin{array}{l}{x=4}\\{y=-8}\end{array}\right.$��$\left\{\begin{array}{l}{x=-4}\\{y=0}\end{array}\right.$���ᣩ��
��������������ĵ�Q������Ϊ��4��-8����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������ƽ���ı��ε��ж������ʣ�����ļ�ֵ��������������⣨1���Ĺؼ��������B��C��D�����꣬�⣨2���Ĺؼ�����x��ʾ��FH���⣨3���Ĺؼ��Ƿ������ۣ���һ���е��Ѷȵ��п������⣮


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0�����������0 | |
| B�� | ��a��-1����$\frac{1}{a}$��a | |
| C�� | ͬ�����������ȡԭ���ķ��ţ����������ľ���ֵ��� | |
| D�� | ��0��a��1����$\frac{1}{a}$��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
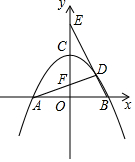 ��ͼ����֪������y=ax2+4��a��0����x�ύ�ڵ�A�͵�B��2��0������y�ύ�ڵ�C����D���������ڵ�һ���ĵ㣮
��ͼ����֪������y=ax2+4��a��0����x�ύ�ڵ�A�͵�B��2��0������y�ύ�ڵ�C����D���������ڵ�һ���ĵ㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
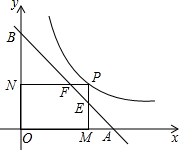 ��ͼ��PΪ����������y=$\frac{3}{2x}$��x��0��ͼ����һ�㣬����P�ֱ���x�ᣬy�������ߣ�����ֱ�ΪM��N��ֱ��y=-x+2��PM��PN�ֱ��ڵ�E��F����x�ᡢy��ֱ���A��B����AF•BE��ֵΪ3��
��ͼ��PΪ����������y=$\frac{3}{2x}$��x��0��ͼ����һ�㣬����P�ֱ���x�ᣬy�������ߣ�����ֱ�ΪM��N��ֱ��y=-x+2��PM��PN�ֱ��ڵ�E��F����x�ᡢy��ֱ���A��B����AF•BE��ֵΪ3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
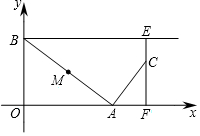 ��ͼ����A��x��Ǹ������ϵĶ��㣬��B����Ϊ��0��4����M���߶�AB���е㣬����M�Ƶ�A˳ʱ�뷽����ת90��õ���C������C��x��Ĵ��ߣ�����ΪF������B��y��Ĵ�����ֱ��CF�ཻ�ڵ�E������AC��BC�����A�ĺ�����Ϊt��
��ͼ����A��x��Ǹ������ϵĶ��㣬��B����Ϊ��0��4����M���߶�AB���е㣬����M�Ƶ�A˳ʱ�뷽����ת90��õ���C������C��x��Ĵ��ߣ�����ΪF������B��y��Ĵ�����ֱ��CF�ཻ�ڵ�E������AC��BC�����A�ĺ�����Ϊt���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com