
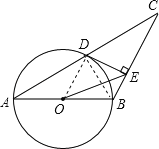
【题目】如图,已知△ABC中,AB=BC,以AB为直径的圆O交AC于点D,过点D作DE⊥BC,垂足为E,连接OE.
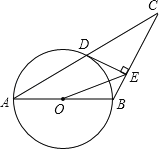
(1)求证:DE是⊙O的切线;
(2)若CD=![]() ,∠ACB=30°,求OE的长.
,∠ACB=30°,求OE的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
试题分析:(1)连接OD、BD,求出BD⊥AC,AD=DC,根据三角形的中位线得出OD∥BC,推出OD⊥DE,根据切线的判定推出即可;
(2)解直角三角形求出BC、BD,求出AB得出OD,根据三角形的面积公式求出高DE,在△ODE中,根据勾股定理求出OE即可.
(1)证明:连接OD、BD,
∵AB是⊙O直径,
∴∠ADB=90°,
∴BD⊥AC,
∵AB=BC,
∴D为AC中点,
∵OA=OB,
∴OD∥BC,
∵DE⊥BC,
∴DE⊥OD,
∵OD为半径,
∴DE是⊙O的切线;
(2)解:∵CD=![]() ,∠ACB=30°,
,∠ACB=30°,
∴cos30°=![]() ,
,
∴BC=2,
∴BD=![]() BC=1,
BC=1,
∵AB=BC,
∴∠A=∠C=30°,
∵BD=1,
∴AB=2BD=2,
∴OD=1,
在Rt△CDB中,由三角形面积公式得:BC×DE=BD×CD,
1×![]() =2DE,
=2DE,
DE=![]() ,
,
在Rt△ODE中,由勾股定理得:OE=![]() =
=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】实验学校九年级一班十名同学定点投篮测试,每人投篮六次,投中的次数统计如下:5,4,3,5,5,2,5,3,4,1,则这组数据的中位数,众数分别为( )
A. 4,5 B. 5,4 C. 4,4 D. 5,5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别写出五边形ABCDE的五个顶点的坐标,然后作出:
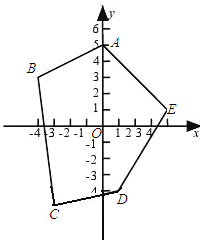
(1)关于原点O对称的图形,并写出对称图形的顶点的坐标;
(2)以原点O为中心,把它缩小为原图形的![]() ,并写出新图形的顶点坐标.
,并写出新图形的顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
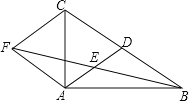
求证:(1)AF=CD;
(2)∠AFC=∠CDA.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是假命题的是( )
A. 有一个角为60°的等腰三角形是等边三角形 B. 等角的补角相等
C. 锐角三角形每个角都小于90° D. 内错角相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com