
分析 设直线l交三角形两边AB,AC于E,F,分三角形ABC的面积比为S1:S2,其对应周长比为P1:P2,有S1:S2=P1:P2.作角A的平分线交EF于O,则O到AB,AC的距离相等,设为d,则S△AEF=$\frac{1}{2}$(AE+AF)d,又S△ABC=$\frac{1}{2}$(a+b+c)r,a,b,c为三边长,r为内切圆半径,只要证明d=r,即可解决问题.
解答 解:设直线l交三角形两边AB,AC于E,F,分三角形ABC的面积比为S1:S2,其对应周长比为P1:P2,有S1:S2=P1:P2.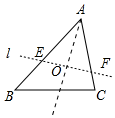
作角A的平分线交EF于O,则O到AB,AC的距离相等,设为d,
则S△AEF=$\frac{1}{2}$(AE+AF)d,又S△ABC=$\frac{1}{2}$(a+b+c)r,a,b,c为三边长,r为内切圆半径,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=$\frac{(AE+AF)d}{(a+b+c)r}$,
∵S1:S2=P1:P2,
∴$\frac{{S}_{△AEF}}{{S}_{△ABC}}$=$\frac{AE+AF}{a+b+c}$,
∴d=r,即O点为内心,
∴直线l过内心O.
点评 本题考查三角形的内切圆与内心、三角形的面积等知识,解题的关键是学会添加常用辅助线,利用比例的性质解决问题,题目比较难,比较抽象.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:选择题
 如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )
如图,某同学把一块三角形玻璃打碎了,现要去买一块大小形状完全相同的玻璃,那么最省事的办法是( )| A. | 带①和②去 | B. | 带①去 | C. | 带②去 | D. | 带③去 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
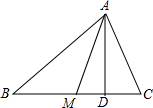 三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )
三角形的一个顶点与对边中点的连线称三角形的中线,这条中线关于这个顶角的平分线对称的直线称为三角形的共轭中线,对于共轭中线下列说法正确的序号是( )| A. | ①② | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
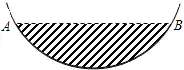 某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).
已知二次函数y=x2+bx+c的图象与y轴交于点C(0,-3),与x轴的一个交点坐标是A(-1,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com