
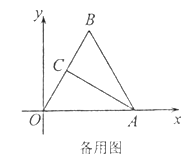
【题目】在平面直角坐标系中,![]() 为坐标原点,点
为坐标原点,点![]() ,点
,点![]() .
.
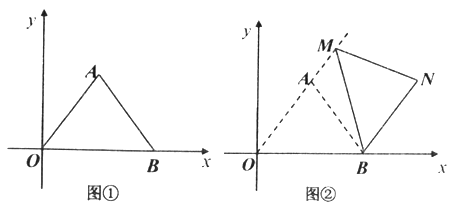
(Ⅰ)如图①,求AB的长;
(Ⅱ)如图②,把图①中的![]() 绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
绕点B顺时针旋转,使点O的对应点AM恰好落在OA延长线上,N是点A旋转后的对应点.
①求证:![]() ;②求点N的坐标;
;②求点N的坐标;
(Ⅲ)点C是OB的中点,点D为线段OA上的动点,在![]() 绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
绕点B顺时针旋转过程中,点D的对应点是P,求线段CP长的取值范围(直接写出结果).
【答案】(Ⅰ)![]() ;(Ⅱ)①见解析,②
;(Ⅱ)①见解析,②![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)过A作![]() ,垂足为C,根据点
,垂足为C,根据点![]() ,点
,点![]() 得出AC和BC的长,再根据勾股得出AB的长
得出AC和BC的长,再根据勾股得出AB的长
(Ⅱ)①根据旋转的性质可得![]() ,再根据等腰三角形的性质可得
,再根据等腰三角形的性质可得![]() ,从而得出
,从而得出![]() ,继而得出结论
,继而得出结论
②过N作![]() 轴,垂足为E.连接AN,根据旋转的性质和一组对边平行且相等的四边形是平行四边形得出四边形AOBN是平行四边形,得出
轴,垂足为E.连接AN,根据旋转的性质和一组对边平行且相等的四边形是平行四边形得出四边形AOBN是平行四边形,得出![]() ,再根据勾股定理求出BE,从而求出点N的坐标;
,再根据勾股定理求出BE,从而求出点N的坐标;
(Ⅲ)过B作CP⊥AO于P,以B为圆心BP为半径画圆交BC于P1,和以B为圆心BO为半径画圆交OB的延长线于P2,得出CP的最大和最小值解答即可;
解:(Ⅰ)过A作![]() ,垂足为C,
,垂足为C,

![]() ,
,
![]()
![]() .
.
在![]() 中,
中,
![]()
(Ⅱ)①由(I)得![]()
由旋转得![]()
![]()
![]()
![]()
![]()

②过N作![]() 轴,垂足为E.连接AN
轴,垂足为E.连接AN
![]() ,
,
∴四边形AOBN是平行四边形。
![]()
在![]() 中,
中,![]() .
.
![]()
![]()
(III)如图,过B作CP⊥AO于P,以B为圆心BP为半径画圆交BC于P1, CP1有最小值,
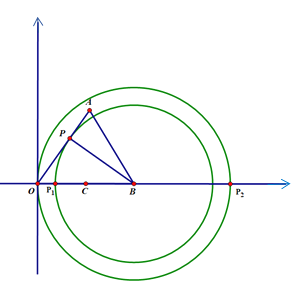
此时![]()
∴BP=![]() ,∴BP1=
,∴BP1=![]() ,
,
∴CP1的最小值为![]() -3=
-3=![]() ;
;
以B为圆心BO为半径画圆交OB的延长线于P2,,CP 2有最大值;
此时CP2=BC +BP2=3+6=9.
线段CP长的取值范围:![]() .
.


 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形![]() 的矩形,点
的矩形,点![]() ,点
,点![]() ,点
,点![]() .以点
.以点![]() 为中心,顺时针旋转矩形
为中心,顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() ,点
,点![]() 旋转后的对应点分别为
旋转后的对应点分别为![]() ,直线
,直线![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
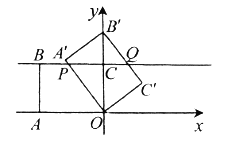
(Ⅰ)如图①,当矩形![]() 的顶点
的顶点![]() 落在
落在![]() 轴正半轴上时,
轴正半轴上时,
(1)求证:![]() ;
;
(2)求点![]() 的坐标.
的坐标.
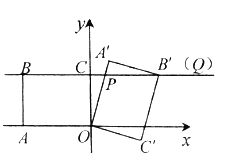
(Ⅱ)如图②,当矩形![]() 的顶点
的顶点![]() 落在直线
落在直线![]() 上时,
上时,
(1)求证:![]() .
.
(2)求点![]() 的坐标.
的坐标.
(Ⅲ)在矩形![]() 旋转过程中,当
旋转过程中,当![]() 时,若
时,若![]() ,请直接写出此时点
,请直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组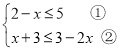
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_____________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=3,点E是边CD的中点,点P,Q分别是射线DC与射线EB上的动点,连结PQ,AP,BP,设DP=t,EQ=![]() t.
t.
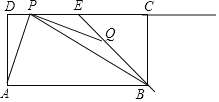
(1)当点P在线段DE上(不包括端点)时.
①求证:AP=PQ;②当AP平分∠DPB时,求△PBQ的面积.
(2)在点P,Q的运动过程中,是否存在这样的t,使得△PBQ为等腰三角形?若存在,请求出t的值;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
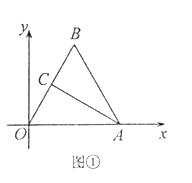
【题目】在平面直角坐标系中,点A(4,0),B为第一象限内一点,且![]() 为等边三角形,C为OB的中点,连接AC.
为等边三角形,C为OB的中点,连接AC.
(I)如图①,求点C的坐标;
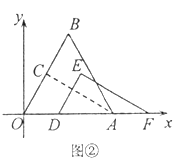
(I)如图②,将![]() 沿x轴向右平移得到
沿x轴向右平移得到![]() ,设
,设![]() ,其中
,其中![]()
①设![]() 与
与![]() 重叠部分的面积为S,用含m的式子表示S:
重叠部分的面积为S,用含m的式子表示S:
②连接![]() ,当
,当![]() 取最小值时,求点E的坐标(直接写出结果即可).
取最小值时,求点E的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形对折后展开(图④是连续两次对折后再展开),再按图示方法折叠,能够得到一个直角三角形(阴影部分),且它的一条直角边等于斜边的一半,这样的图形有( ).

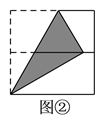


A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com