

���� ��1�����۵������ʿ�֪��PE=BE����EPH=��ABC=90�㣬�Ӷ���֤����EBP=��EPB����Ȼ���ٸ��ݡ�EPH-��EPB=��EBC-��EBP���õ���PBC=��BPH����ƽ���ߵ����ʿ�֪����APB=��PBC���Ӷ���֤����APB=��BPH��
��2������B��BH��PH���ֱ�֤��Rt��APB��Rt��MPB��Rt��BMH��Rt��BCH���Ӷ���֪��AP=PM��MH=CH���Ӷ���֤��������PDH���ܳ�=AD+DC=8��
��3������F��FN��AB������ΪN����֤����EFN�ա�BPA���Ӷ��õ���EN=AP=x��Ȼ����Rt��APE�У��ɹ��ɶ�������ã�BE=2+$\frac{{x}^{2}}{8}$���Ӷ��õ�CF=BE-EN=2+$\frac{{x}^{2}}{8}-x$����Ϊ�ı���PEFG���ı���BEFCȫ������S=$\frac{1}{2}$��EF+CF��BC���Ӷ��ɵõ�S=$\frac{1}{2}{x}^{2}-2x+8$����������䷽��������ú�������ֵ��
��� �⣺��1����ͼ1��ʾ��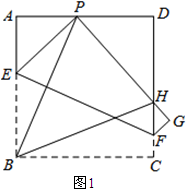
֤�������۵������ʿ�֪��PE=BE����EPH=��ABC=90�㣬
���EBP=��EPB��
���EPH-��EPB=��EBC-��EBP��������PBC=��BPH��
�֡�AD��BC��
���APB=��PBC��
���APB=��BPH��
��2�����仯��
���ɣ���ͼ2����B��BH��PH��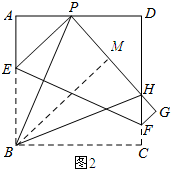
��Rt��APB��Rt��MPB��$\left\{\begin{array}{l}{��A=��PMB}\\{��APB=��BPM}\\{PB=PB}\end{array}\right.$��
��Rt��APB��Rt��MPB��
��AP=PM��BM=AB��
���ı���ABCDΪ�����Σ�
��AB=BC��
��MB=BC��
��Rt��BMH��Rt��BCH��$\left\{\begin{array}{l}{BH=BH}\\{BM=BC}\end{array}\right.$��
��Rt��BMH��Rt��BCH��
��MH=CH��
��PD+PH+DH=PD+PM+MH+DH=PD+PA+DH+HC=AD+DC=8��
��������PDH���ܳ����䣮
��3����ͼ3������F��FN��AB������ΪN����FN=BC=AB��
��EFΪ�ۺۣ�
��EF��BP��
���EFN+��NEF=��ABP+��BEF=90�㣮
���EFN=��ABP��
�֡ߡ�A=��ENF=90�㣬
�ڡ�EFN�͡�BPA��$\left\{\begin{array}{l}{��EFN=��ABP}\\{AB=FN}\\{��A=��ENF}\end{array}\right.$��
���EFN�ա�BPA��
��EN=AP=x��
��AE+BE=4��
��AE=4-BE��
��Rt��APE�У��ɹ��ɶ�����֪��AE2+AP2=EP2��
�֡�EP=EB��
�ࣨ4-BE��2+x2=BE2��
��ã�BE=2+$\frac{{x}^{2}}{8}$��
��CF=BE-EN=2+$\frac{{x}^{2}}{8}-x$��
���ı���PEFG���ı���BEFCȫ�ȣ�
��S=$\frac{1}{2}$��EF+CF��BC=$\frac{1}{2}��4+\frac{{x}^{2}}{4}-x����4$����S=$\frac{1}{2}{x}^{2}-2x+8$��
�䷽�ã�S=$\frac{1}{2}��x-2��^{2}+6$
�൱x=2ʱ��S����Сֵ����СֵΪ6��
���� ���⿼����������Ρ��ı��κͺ������ۺ�Ӧ�ã�֤��������DPH���ܳ�����AD+DC�Լ����BE��CF�ij����ú�x��ʽ�ӱ�ʾ���ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������30���ֱ�����dz߷�����ͼ��ʾ��ֱ������ϵ�У���A��0��4������B��ԭ�㣬��C=90�㣬��ABC=30�㣬D����A�����ԭ��Գƣ�A����D���˶�������D���ֹͣ��B����x�����˶�����A����Dʱ����C�߹���·����Ϊ4$\sqrt{3}$��
��ͼ������30���ֱ�����dz߷�����ͼ��ʾ��ֱ������ϵ�У���A��0��4������B��ԭ�㣬��C=90�㣬��ABC=30�㣬D����A�����ԭ��Գƣ�A����D���˶�������D���ֹͣ��B����x�����˶�����A����Dʱ����C�߹���·����Ϊ4$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
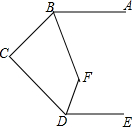 ��ͼ����֪AB��DE��BC��CD����ABC�͡�CDE��ƽ���߽��ڵ�F����BFD=135�㣮
��ͼ����֪AB��DE��BC��CD����ABC�͡�CDE��ƽ���߽��ڵ�F����BFD=135�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
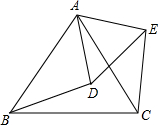 ��ͼ����֪��ABC�ǵȱ������Σ���ABD�Ƶ�A��ת����ACE��λ�ã�����DE����AD=5�����ADE���ܳ���
��ͼ����֪��ABC�ǵȱ������Σ���ABD�Ƶ�A��ת����ACE��λ�ã�����DE����AD=5�����ADE���ܳ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com