
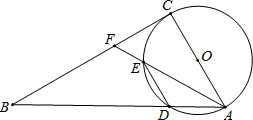
 如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC.
如图,以Rt△ABC的边AC为直径的⊙O交斜边AB于点D,点F为BC上一点,AF交⊙O于点E,且DE∥AC. |
| CE |
 |
| AD |
 |
| CD |
 |
| AE |
| 1 |
| 2 |
| 1 |
| 2 |
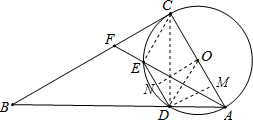 (1)证明:连接CE,
(1)证明:连接CE, |
| CE |
 |
| AD |
 |
| CD |
 |
| AE |
|
8
| ||
| 5 |
16
| ||
| 5 |
| 1 |
| 2 |
| 1 |
| 2 |
| AD•BD |
| AB |
| ||||||||
| 8 |
| 16 |
| 5 |
| OD2-ON2 |
42-(
|
| 12 |
| 5 |
| 24 |
| 5 |


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
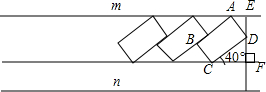 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.| A、8.6 | B、5.2 |
| C、4.8 | D、5.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
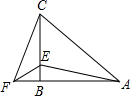 在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且
如图,已知D、E分别是△ABC中AB、AC边上的点,DE∥BC且| AD |
| AB |
| 1 |
| 3 |
| A、4 | B、6 | C、8 | D、18 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| OF+AG |
| FG |
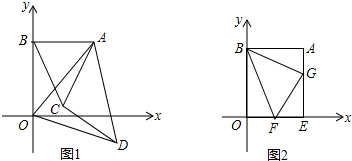
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com