
【题目】如图,矩形ABCD中,点E、F、G. H分别AB、BC、 CD、 DA边上的动点,且AE=BF=CG=DH

(1)求证:四边形EFGH是平行四边形:
(2)在点E、F、G、H运动过程中,判断直线GE是否经过某一定点,如果是,请你在图中画出这个点:如果不是,请说明理由.
【答案】(1)证明见解析;(2)是,直线GE总过AC、BD的交点M,作图见解析.
【解析】
(1)由矩形的性质得出∠A=∠C=90°,BC=AD,由AE=BF=CG=DH证出AH=CF,由SAS证明△AEH≌△CGF,可得HE=FG,同理可得HG=FE即可求解;
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.只要证明四边形AECG是平行四边形,即可推出MA=MG,MG=ME,即点M为AC的中点,又矩形ABCD的对角线互相平分,推出点M为矩形对角线ACBD的交点.
解:(1)∵四边形ABCD为矩形,
∴BC=AD,∠A=∠C=90°,
∵BF=DH,
∴BC-BF=AD-DH,即CF=AH,
又AE=CG,
∴△HAE≌△FCG,
∴HE=FG,
同理可证:HG=FE,
∴四边形EFGH是平行四边形.
(2)直线GE经过一个定点,这个定点为矩形的对角线AC、BD的交点.
理由如下:
如图,连结AC、AG、CE,设AC、EG的交点为M.
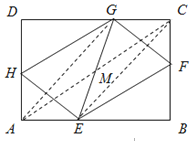
∵AE∥CG,AE=CG,
∴四边形AECG是平行四边形,
∴MA=MG,MG=ME,
即点M为AC的中点,
又矩形ABCD的对角线互相平分
∴点M为矩形对角线ACBD的交点,
∴直线GE总过AC、BD的交点M.


科目:初中数学 来源: 题型:
【题目】在数学课上,老师提出利用尺规作图完成下面问题:

已知:∠ACB是△ABC的一个内角.
求作:∠APB=∠ACB.
小路的作法如下:

老师说:“小路的作法正确.”
请回答:(1)点O为△ABC外接圆圆心(即OA=OB=OC)的依据是_____;
(2)∠APB=∠ACB的依据是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线AB与x轴、y轴相交于![]() 、
、![]() 两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转
两点,动点C在线段OA上(不与O、A重合),将线段CB绕着点C顺时针旋转![]() 得到CD,当点D恰好落在直线AB上时,过点D作
得到CD,当点D恰好落在直线AB上时,过点D作![]() 轴于点E.
轴于点E.

(1)求证,![]() ;
;
(2)如图2,将![]() 沿x轴正方向平移得
沿x轴正方向平移得![]() ,当直线
,当直线![]() 经过点D时,求点D的坐标及
经过点D时,求点D的坐标及![]() 平移的距离;
平移的距离;

(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年5月16日,第十五届文博会在深圳拉开帷幕,周末,小明骑共享单车从家里出发去分会馆参观,途中突然发现钥匙不见了,于是原路折返,在刚才等红绿灯的路口找到了钥匙,便继续前往分会馆,设小明从家里出发到分会场所用的时间为x(分钟),离家的距离为y(米),且x与y的关系示意图如图所示,请根据图中提供的信息回答下列问题:
(1)图中自变量是 .因变量是 .
(2)小明等待红绿灯花了 分钟.
(3)小明的家距离分会馆 米
(4)小明在 时间段的骑行速度最快,最快速度是 米/分钟.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,点
中,点![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() ,
,![]() 上的点,且
上的点,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,若点
,若点![]() 是
是![]() 的重心.则以下结论:①线段
的重心.则以下结论:①线段![]() ,
,![]() ,
,![]() 是
是![]() 的三条角平分线;②
的三条角平分线;②![]() 的面积是
的面积是![]() 面积的一半;③图中与
面积的一半;③图中与![]() 面积相等的三角形有5个;④
面积相等的三角形有5个;④![]() 的面积是
的面积是![]() 面积的
面积的![]() .其中一定正确的结论有( )
.其中一定正确的结论有( )

A.①②③B.②④C.③④D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】彩虹服装店用![]() 元购进
元购进![]() 件衬衣,很快全部售完.服装店老板以每件
件衬衣,很快全部售完.服装店老板以每件![]() 元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:
元的价格为标准,将超出的记为正数,不足的记为负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元).他卖完这
(单位:元).他卖完这![]() 件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
件衬衣后是盈利还是亏损?盈利(或亏损)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=24,BC=26,CA=14.顺次连接△ABC各边中点,得到△A1B1C1;再顺次连接△A1B1C1各边中点,得到△A2B2C2…如此进行下去,得到![]() ,则△A8B8C8的周长为( )
,则△A8B8C8的周长为( )

A.1B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=9,AC=6,BC=12,点M在AB边上,且AM=3,过点M作直线MN与AC边交于点N,使截得的三角形与原三角形相似,则MN=__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC中, AO是∠BAC的角平分线, D为 AO上一点,以 CD为一边且在 CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE.
(2)延长BE至Q, P为BQ上一点,连接 CP、CQ使 CP=CQ=5,若 BC=6,求PQ的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com