
分析 根据互余的定义,可得∠COD的度数,根据角平分线的性质,可得∠BOC的度数,根据角的和差,可得答案.
解答 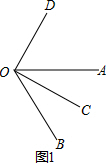 解:如图1,
解:如图1,
由∠AOD与∠AOC互余,得∠COD=90°,
∵OC平分∠AOB,
∴∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×64°=32°.
由角的和差,得∠BOD=∠COD+∠BOC=90°+32°=122°.
如图2,
由∠AOD与∠AOC互余,得∠COD=90°,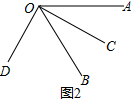 ∵OC平分∠AOB,
∵OC平分∠AOB,
∴∠BOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×64°=32°.
由角的和差,得∠BOD=∠COD-∠BOC=90°-32°=58°.
故答案为:122°或58°.
点评 本题考查了余角和补角,角平分线的定义,利用了互余的定义,角平分线的定义,角的和差,以及分类思想的运用.


科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
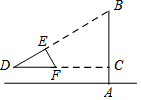 如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
如图,小南用自制的直角三角形纸板DEF测量树的高度AB,他使斜边DF保持水平,并且边DE与点B在同一直线上.己知三角形的两条直角边DE=0.6m,EF=0.3m,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
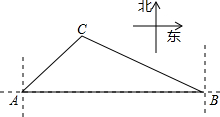 如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.
如图,一艘海轮在A点时测得灯塔C在它的北偏东45°方向上,它沿正东方向航行80海里后到达B处.此时灯塔C在它的北偏西60°方向上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
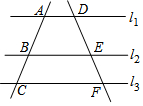 如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.
如图,直线l1∥l2∥l3,直线AC依次交l1、l2、l3于A、B、C三点,直线DF依次交l1、l2、l3于D、E、F三点,若$\frac{AB}{AC}$=$\frac{4}{7}$,DE=2,求EF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com