
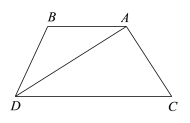
【题目】如图,已知AB∥CD,AD平分∠BDC.
(1)求证:∠BAD=∠BDA;
(2)若AD⊥AC,∠C=700,求∠B的度数.
【答案】(1)见解析;(2)140°.
【解析】
(1)由AB∥CD可得∠BAD=∠CDA,由AD平分∠BDC可得∠CDA=∠BDA,两者结合即可得到∠BAD=∠BDA;
(2)由AD⊥AC可得∠DAC=90°,结合∠C=70°可得∠CDA=20°,结合AD平分∠BDC可得∠BDC=40°,再结合AB∥CD即可得到∠B=140°.
(1)∵AB∥CD,
∴∠BAD=∠ADC,
∵AD平分∠BDC,
∴∠BDA=∠ADC,
∴∠BAD=∠BDA;
(2)∵AB∥CD
∴∠B+∠BDC=180°,
∵AD⊥AC,∠C=70°,
∴∠ADC=180°-70°-90°=20°,
∵AD平分∠BDC,
∴∠BDC=2∠ADC=40°,
∴∠B=180°-∠BDC=180°-40°=140°.


科目:初中数学 来源: 题型:
【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家樱桃采摘园的品质相同,销售价格也相同,“五一期间”,两家均推出了优惠方案,甲采摘园的优惠方案是:游客进园需购买50元的门票,采摘的草莓六折优惠;乙采摘园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,设某游客的草莓采摘量为x(千克),在甲采摘园所需总费用为y1(元),在乙采摘园所需总费用为y2(元),图中折线OAB表示y2与x之间的函数关系. 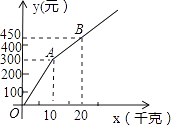
(1)甲、乙两采摘园优惠前的草莓销售价格是每千克元;
(2)求y1、y2与x的函数表达式;
(3)在图中画出y1与x的函数图象,若某人想在“五一期间”采摘樱桃25千克,那么甲、乙哪个采摘园较为优惠?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,
, ![]() ,
, ![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 点的坐标.
点的坐标.
(![]() )如图
)如图![]() ,
, ![]() 为
为![]() 轴负半轴上一个动点,当
轴负半轴上一个动点,当![]() 点沿
点沿![]() 轴负半轴向下运动时,以
轴负半轴向下运动时,以![]() 为顶点,
为顶点, ![]() 为腰作等腰
为腰作等腰![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,求
点,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中, ![]() ,
, ![]() 为线段
为线段![]() 上一点,
上一点, ![]() ,
, ![]() 为射线
为射线![]() 上一点,且
上一点,且![]() ,连接
,连接![]() .
.
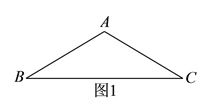
(![]() )如图
)如图![]() ,
,
①依题意补全图形.
②若![]() ,
, ![]() ,求
,求![]() 的长.
的长.
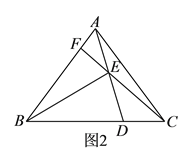
(![]() )如图
)如图![]() ,若
,若![]() ,连接
,连接![]() 并延长,交
并延长,交![]() 于点
于点![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
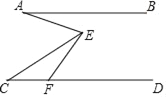
【题目】如图,已知AB∥CD,F为CD上一点,∠EFD=60°,∠AEC=2∠CEF,若6°<∠BAE<15°,∠C的度数为整数,则∠C的度数为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,∠A,∠B,∠C的对边分别为a、b、c,下列说法中错误的是( )
A.如果∠C-∠B=∠A,则△ABC是直角三角形,且∠C=90;
B.如果![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
C.如果(c+a)( c-a)=![]() ,则△ABC是直角三角形,且∠C=90;
,则△ABC是直角三角形,且∠C=90;
D.如果∠A:∠B:∠C=3:2:5,则△ABC是直角三角形,且∠C=90.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,在直角坐标系xOy中,A(﹣1,0),B(3,0),将A,B同时分别向上平移2个单位,再向右平移1个单位,得到的对应点分别为D,C,连接AD,BC.

(1)直接写出点C,D的坐标:C ,D ;
(2)四边形ABCD的面积为 ;
(3)点P为线段BC上一动点(不含端点),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com