
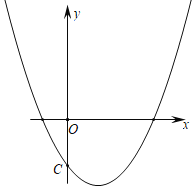
【题目】已知:抛物线y=x2﹣2x+m与y轴交于点C(0,﹣2),点D和点C关于抛物线对称轴对称.
(1)求此抛物线的解析式和点D的坐标;
(2)如果点M是抛物线的对称轴与x轴的交点,求MCD的周长.
【答案】(1)y=x2﹣2x﹣2,点D的坐标为(2,﹣2);(2)2+2![]() .
.
【解析】
(1)利用二次函数图象上点的坐标特征可求出m值,进而可得出抛物线的解析式,由抛物线的解析式利用二次函数的性质可得出抛物线的对称轴,结合点C的坐标可得出点D的坐标;
(2)求得M点的坐标,然后根据勾股定理求得MC=MD=![]() ,即可求得△MCD的周长为:2+2
,即可求得△MCD的周长为:2+2![]() .
.
(1)抛物线y=x2﹣2x+m与y轴交于点C(0,﹣2),
∴m=﹣2,
∴此抛物线的解析式为y=x2﹣2x﹣2,
∵抛物线的解析式为y=x2﹣2x﹣2=(x﹣1)2﹣3,
∴抛物线的对称轴为直线x=1.
∵点D与C关于抛物线的对称轴对称,
∴点D的坐标为(2,﹣2).
(2)∵抛物线的对称轴为直线x=1.
∴M(1,0),
∴MC=MD=![]() =
=![]()
∵CD=2,
∴△MCD的周长为:2+2![]() .
.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
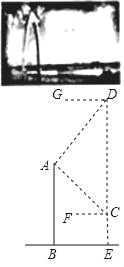
【题目】通达桥即小店汾河桥,是太原新建成的一座跨汾大桥,也是太原首座悬索桥.桥的主塔由曲线形拱门组成,取意“时代之门”.无人机社团的同学计划利用无人机设备测量通达桥拱门的高度.如图,他们先将无人机升至距离桥面50米高的点C处,测得桥的拱门最高点A的仰角∠ACF为30°,再将无人机从C处竖直向上升高200米到点D处,测得点A的俯角∠ADG为45°.已知点A,B,C,D,E在同一平面内,求通达桥拱门最高点A距离桥面BE的高度AB.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC是路边坡角为30°,长为10米的一道斜坡,在坡顶灯杆CD的顶端D处有一探射灯,射出的边缘光线DA和DB与水平路面AB所成的夹角∠DAN和∠DBN分别是37°和60°(图中的点A、B、C、D、M、N均在同一平面内,CM∥AN).
(1)求灯杆CD的高度;
(2)求AB的长度(结果精确到0.1米).(参考数据:![]() =1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)
=1.73.sin37°≈060,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
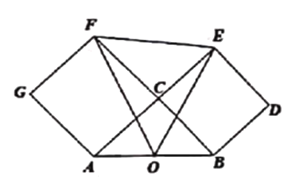
【题目】我们知道,勾股定理反映了直角三角形三条边的关系: a2+b2=c2, 而a2, b2, c2又可以看成是以a,b, c为边长的正方形的面积.如图,在Rt△ABC中,∠ACB=90°,BC=a, AC=b,O为AB的中点.分别以AC,BC 为边向△ABC外作正方形ACFG,BCED,连结OF, EF, OE,则△OEF的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
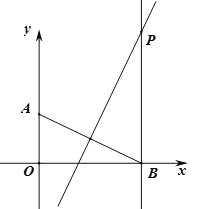
【题目】如图,在平面直角坐标系中,y轴上一点A(0,2),在x轴上有一动点B,连结AB,过B点作直线l⊥x轴,交AB的垂直平分线于点P(x,y),在B点运动过程中,P点的运动轨迹是________,y关于x的函数解析式是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
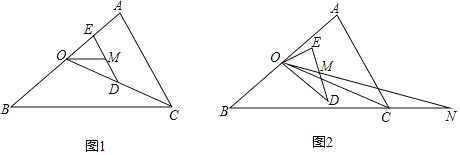
【题目】如图,OC是△ABC中AB边的中线,∠ABC=36°,点D为OC上一点,如果OD=kOC,过D作DE∥CA交于BA点E,点M是DE的中点,将△ODE绕点O顺时针旋转α度(其中0°<α<180°)后,射线OM交直线BC于点N.
(1)如果△ABC的面积为26,求△ODE的面积(用k的代数式表示);
(2)当N和B不重合时,请探究∠ONB的度数y与旋转角α的度数之间的函数关系式;
(3)写出当△ONB为等腰三角形时,旋转角α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店老板到厂家选购![]() 、
、![]() 两种品牌的羽绒服,
两种品牌的羽绒服,![]() 品牌羽绒服每件进价比
品牌羽绒服每件进价比![]() 品牌羽绒服每件进价多
品牌羽绒服每件进价多![]() 元,若用
元,若用![]() 元购进
元购进![]() 种羽绒服的数量是用
种羽绒服的数量是用![]() 元购进
元购进![]() 种羽绒服数量的
种羽绒服数量的![]() 倍.
倍.
(1)求![]() 、
、![]() 两种品牌羽绒服每件进价分别为多少元?
两种品牌羽绒服每件进价分别为多少元?
(2)若![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,
元,![]() 品牌羽绒服每件售价为
品牌羽绒服每件售价为![]() 元,服装店老板决定一次性购进
元,服装店老板决定一次性购进![]() 、
、![]() 两种品牌羽绒服共
两种品牌羽绒服共![]() 件,在这批羽绒服全部出售后所获利润不低于
件,在这批羽绒服全部出售后所获利润不低于![]() 元,则最少购进
元,则最少购进![]() 品牌羽绒服多少件?
品牌羽绒服多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点![]() 在反比例函数
在反比例函数![]() 的图象上,过点
的图象上,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,直线
,直线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() .
.

(1)求反比例函数![]() 和一次函数
和一次函数![]() 的表达式;
的表达式;
(2)直接写出关于![]() 的不等式
的不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,AB=2,BC=m,点E是边BC上一点,BE=1,连接AE,沿AE翻折△ABE使点B落在点F处.
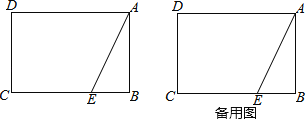
(1)连接CF,若CF∥AE,求m的值;
(2)连接DF,若![]() ≤DF≤
≤DF≤![]() ,求m的取值范围.
,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com