
认真阅读下面关于三角形内、外角平分线所夹的 探究片段,完成所提出的问题.
探究片段,完成所提出的问题.
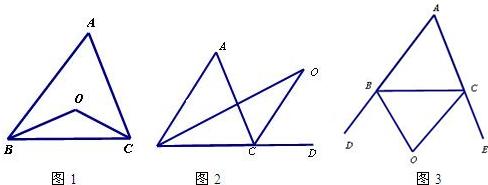
探究1:如图1,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90°+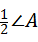 ,理由如下:
,理由如下:
∵ BO和CO分别是∠ABC和∠ACB的角平分线,
∴ .
.
∴ 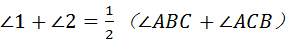 .
.
又∵∠ABC+∠ACB=180°﹣∠A,
∴ 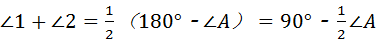 .
.
∴ ∠BOC=180°﹣(∠1+∠2)=180°﹣(90°﹣ ∠A)
∠A)
=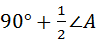 .
.
探究2:如图2中,O是 ∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ABC与外角∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
探究3:如图3中,O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(只写结论,不需证明)
结论: .
|
分析:(1)根据提供的信息,根据三角形的一个外角等于与它不相邻的两个内角的和,用∠A与∠1表示出∠2,再利用∠O与∠1表示出∠2,然后整理即可得到∠BOC与∠O的关系;
(2)根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB,然后再根据三角形的内角和定理列式整理即可得解.
解:(1)探究2结论:∠BOC= ∠A,
∠A,
理由如下:
∵ BO和CO分别是∠ABC和∠ACD的角平分线,
∴∠1= ∠ABC,∠2=
∠ABC,∠2= ∠ACD,
∠ACD,
又∵∠ACD是△ABC的 一外角,
一外角,
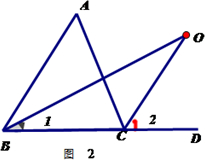 ∴∠ACD=∠A+∠ABC,
∴∠ACD=∠A+∠ABC,
∴∠2= (∠A+∠ABC)=
(∠A+∠ABC)= ∠A+∠1,
∠A+∠1,
∵∠2是△BOC的一外角,
∴∠BOC=∠2﹣∠1= ∠A+∠1﹣∠1=
∠A+∠1﹣∠1= ∠A;
∠A;
(2)探究3:∠OBC= (∠A+∠ACB),∠OCB=
(∠A+∠ACB),∠OCB= (∠A+∠ABC),
(∠A+∠ABC),
∠BOC=180°﹣∠0BC﹣∠OCB,
=180°﹣ (∠A+∠ACB)﹣
(∠A+∠ACB)﹣ (∠A+∠ABC),
(∠A+∠ABC),
=180°﹣ ∠A﹣
∠A﹣ (∠A+∠ABC+∠ACB),
(∠A+∠ABC+∠ACB),
结论∠BOC=90°﹣ ∠A.
∠A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
2012年我市某县筹备20周年县庆,园林部门决定利用现有的3 490盆甲种花卉和2 950盆乙种花卉搭配 两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个
两种园艺造型共50个摆放在迎宾大道两侧,已知搭配一个 种造型需甲种花卉80盆,乙种花卉40盆,搭配一个
种造型需甲种花卉80盆,乙种花卉40盆,搭配一个 种造型需甲种花卉50盆,乙种花卉90盆.
种造型需甲种花卉50盆,乙种花卉90盆.
(1)某校九年级(1)班课外活动小组承接了这个园艺造型搭配方案的设计,问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个 种造型的成本是800元,搭配一个
种造型的成本是800元,搭配一个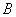 种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
种造型的成本是960元,试说明(1)中哪种方案成本最低?最低成本是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com