
【题目】在△ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为 . 
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在等腰Rt△ABC中,∠ACB=90°,D为BC的中点,DE⊥AB,垂足为E,过点B作BF∥AC交DE的延长线于点F,连接CF.
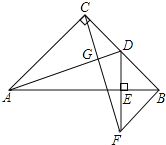
(1)求证:AD⊥CF;
(2)连接AF,试判断△ACF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 l 与 x 轴, y 轴分别交于 M,N 两点,且 OM=ON=3.
(1)求这条直线的函数表达式;
(2)Rt△ ABC 与直线 l 在同一个平面直角坐标系内,其中∠ABC=90°,AC= 2![]() ,A(1,0),B(3,0),将△ABC 沿 x 轴向左平移,当点 C 落在直线 l 上时,求线段 AC 扫过的面积.
,A(1,0),B(3,0),将△ABC 沿 x 轴向左平移,当点 C 落在直线 l 上时,求线段 AC 扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
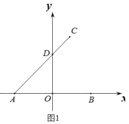
【题目】如图 1,在平面直角坐标系中,已知点A(a,0),B(b,0),C(2,7),连接 AC,交y轴于 D,且![]() ,
,![]() .
.
(1)求点D的坐标.
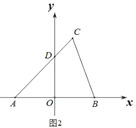
(2)如图 2,y轴上是否存在一点P,使得△ACP的面积与△ABC的面积相等?若存在,求点P的坐标,若不存在,说明理由.
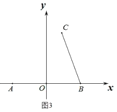
(3)如图 3,若 Q(m,n)是 x轴上方一点,且![]() 的面积为20,试说明:7m+3n是否为定值,若为定值,请求出其值,若不是,请说明理由.
的面积为20,试说明:7m+3n是否为定值,若为定值,请求出其值,若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.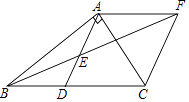
(1)证明四边形ADCF是菱形;
(2)若AC=4,AB=5,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥BC,DC⊥BC,垂足分别为B、C,设AB=4,DC=1,BC=4.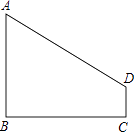
(1)求线段AD的长.
(2)在线段BC上是否存在点P,使△APD是等腰三角形?若存在,求出线段BP的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
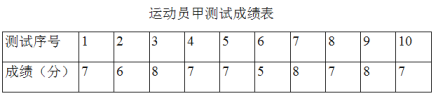
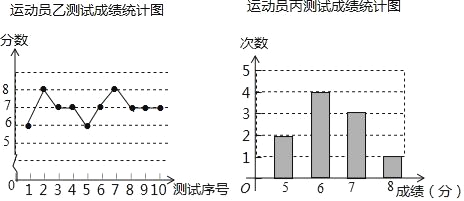
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、S丙2=0.8)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com