
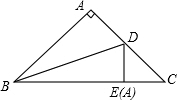
 如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.
如图,等腰直角△ABC中,∠A=90°,AB=AC,把等腰直角△ABC沿BD折叠,使点A落在边BC上的点E处,CE=1,求BC的长.| 2 |
| 2 |
 解:如图,由题意得:
解:如图,由题意得:| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


科目:初中数学 来源: 题型:
| 25 |
| 2 |
| 11 |
| 3 |
| π |
| 3 |
| •• |
| 25 |
| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
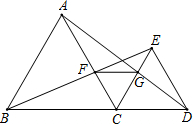 如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论?
如图,已知点C在线段BD上,在BD的同侧作正△CDE、正△ABC,AC交BE于F,AD交CE于G,连接FG,在这个图形中,不在标注其它字母和添加任何辅助线,由这些条件可推出哪些结论?查看答案和解析>>
科目:初中数学 来源: 题型:
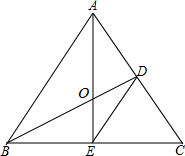 如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.
如图,△ABC是等边三角形,BD⊥AC,AE⊥BC,垂足分别为D、E,AE、BD相交于点O,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=
如图,等边△ABC中,D、E分别在AB、BC边上,且AD=2BE=4,连接DE,并将线段DE绕点E顺时针旋转60°,得到线段EF,连接CF,取EF中点G,连接AG,延长CF交AG于点H.若AH=| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
A、“掷一枚硬币正面朝上的概率是
| ||
| B、一组数据2,2,3,6的众数和中位数都是2 | ||
| C、要了解全市人民的低碳生活状况,适宜采用抽样调查的方法 | ||
| D、随机抽取甲、乙两名同学的5次数学成绩,计算得平均分都是90分,方差分别是S2甲=5,S2乙=12,说明乙的成绩较为稳定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com