Question

已知抛物线y=ax²+bx+c与y轴交于点A（0，3），与x轴分别交于B（1，0）、C（5，0）两点．
（1）求此抛物线的解析式；
（2）若点D为线段OA的一个三等分点，求直线DC的解析式；
（3）若一个动点P自OA的中点M出发，先到达x轴上的某点（设为点E），再到达抛物线的对称轴上某点（设为点F），最后运动到点A′求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．

Answer 1

分析：（1）由于A、B、C三点的坐标已知，代入函数解析式中利用待定系数法就可以确定函数的解析式；
（2）若点D为线段OA的一个三等分点，那么根据已知条件可以确定D的坐标为（0，1）或，（0，2），而C的坐标已知，利用待定系数法就可以确定直线CD的解析式；
（3）如图，由题意，可得M（0，

3

2

），点M关于x轴的对称点为M′（0，-

3

2

），点A关于抛物线对称轴x=3的对称点为A'（6，3），连接A'M'，根据轴对称性及两点间线段最短可知，A'M'的长就是所求点P运动的最短总路径的长，根据待定系数法可求出直线A'M'的解析式为y=

3

4

x-

3

2

，从而求出E、F两点的坐标，再根据勾股定理可以求出A'M'=

15

2

，也就求出了最短总路径的长．

解答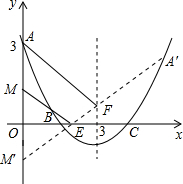：解：（1）根据题意，c=3，
所以

a+b+3=0 25a+5b+3=0

解得

a= 3 5 b=- 18 5

所以抛物线解析式为y=

3

5

x²-

18

5

x+3．

（2）依题意可得OA的三等分点分别为（0，1），（0，2）．
设直线CD的解析式为y=kx+b．
当点D的坐标为（0，1）时，直线CD的解析式为y=-

1

5

x+1；
当点D的坐标为（0，2）时，直线CD的解析式为y=-

2

5

x+2．

（3）如图，由题意，可得M（0，

3

2

）．
∵点M关于x轴的对称，
∴点为M′（0，-

3

2

），
∴点A关于抛物线对称轴x=3的对称点为A'（6，3）．
连接A'M'．
根据轴对称性及两点间线段最短可知，A'M'的长就是所求点P运动的最短总路径的长．
∴A'M'与x轴的交点为所求E点，与直线x=3的交点为所求F点．
∴可求得直线A'M'的解析式为y=

3

4

x-

3

2

．
∴可得E点坐标为（2，0），F点坐标为（3，

3

4

）．
由勾股定理可求出A′M′=

15

2

．
∴点P运动的最短总路径（ME+EF+FA）的长为

15

2

．（8分）

点评：本题着重考查了待定系数法求二次函数解析式，一次函数的解析式，图形的对称变换，求最短线段之和等重要知识点，综合性强，能力要求极高．考查学生分类讨论，数形结合的数学思想方法．