
【题目】在平面直角坐标系中,点A的坐标为![]() .
.
(1)如图1,若点B 在x轴正半轴上,点![]() ,
,![]() ,
,![]() ,求点B坐标;
,求点B坐标;
(2)如图2,若点B 在x轴负半轴上,![]() 轴于点E,
轴于点E,![]() 轴于点F,
轴于点F,![]() ,MF交直线AE于点M,若点
,MF交直线AE于点M,若点![]() ,BM=5,求点M坐标.
,BM=5,求点M坐标.

【答案】(1)B(4,0);(2)M(3,-3)
【解析】
(1)作AD⊥x轴,CE⊥x轴,垂足分别为D、E,先利用AAS定理证明△ADB≌△BEC得出BD=CE,从而求出OD,CE,最后进一步求解即可;
(2)在AM上截取AN=OB,连接FN,先后根据SAS定理证明△BOF≌△NAF与△BFM≌△NFM,然后进一步求出NM,AN的值,最后根据题求解即可.
(1)如图1:作AD⊥x轴,CE⊥x轴,垂足分别为D、E,
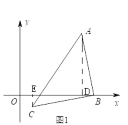
∴∠ADB=∠BEC=90°,
∴∠DAB+∠ABD=90°,
∵AB⊥BC,
∴∠EBC+∠ABD=90°,
∴∠DAB=∠ABC,
在△ADB与△BEC中,
∵∠ADB=∠BEC,∠DAB=∠EBC,AB=BC,
∴△ADB≌△BEC(AAS),
∴BD=CE,
∵A(3,3),C(-1,1),
∴OD=3,CE=1,
∴OB=OD+BD=OD+CE=3+1=4,
∴B点坐标为(4,0).
(2)如图2:在AM上截取AN=OB,连接FN,
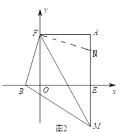
∵A(3,3),
∴OF=AF=OE=3,
在△BOF与△NAF中,
∵AN=OB,∠A=∠BOF,OF=AF,
∴△BOF≌△NAF(SAS),
∴BF=NF,∠BFO=∠NFA,
∵∠BFM=∠BFO+∠OFM=45°,
∴∠NFA+∠OFM=45°,
∴∠OFA=90°,
∴∠NFM=∠OFA-∠NFA-∠OFM=45°,
∴∠BFM=∠NFM,
在△BFM与△NFM中,
∵BF=AN,∠BFM=∠NFM,FM=FM,
∴△BFM≌△NFM(SAS),
∴BM=NM,
∵BM=5,B(-1,0),
∴NM=5,OB=AN=1,
∴EM=AN+NM-AE=3,
∴M点坐标为(3,-3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,∠BAC=30°,延长BC至D使CD=BC,连接AD,且AD=4,点P为线段AC上一动点,连接BP.则2BP+AP的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E到△ABC三边的距离相等,过点E作MN∥BC交AB于M,交AC于N.若BM+CN=2019,则线段NM的长为( )

A.2017B.2018C.2019D.2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )

A.![]() B.
B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:

(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长度为1个单位长度的小正方形组成的正方形网格中,点 A,B,C 在小正方形的顶点上.

(1)在图中画出与△ ABC 关于直线 l 成轴对称的△ AB′C ′;
(2)请在直线 l 上找到一点 P,使得 PC+PB 的距离之和最小,在图中画出点P的位置,并求出这个最小距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C在⊙O上,AD垂直于过点C的切线,垂足为D,CE垂直AB,垂足为E.延长DA交⊙O于点F,连接FC,FC与AB相交于点G,连接OC.
(1)求证:CD=CE;
(2)若AE=GE,求证:△CEO是等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(-1,5),B(-2,0),C(-4,3).
(1)请画出△ABC关于y轴对称的△A,B,C,,并写出点C的坐标;
(2)求△ABC的面积;
(3)在y轴上画出点P的位置,使线段PA+PB的值最小,并直接写出PA+PB的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com