
分析 分两种情况①当x>-1时,y=$\sqrt{3}$x+$\sqrt{3}$,设P(x,$\sqrt{3}$x+$\sqrt{3}$),作AM⊥y轴于M,PN⊥y轴于N,根据S=S梯形ANMP-S△POM-S△PON即可求得;②当x<-1时,y=-$\sqrt{3}$x-$\sqrt{3}$,设P(x,-$\sqrt{3}$x-$\sqrt{3}$),作AN⊥x轴于N,PM⊥x轴于M,根据S=S梯形ANMP-S△POM-S△PON即可求得.
解答 解:∵点P是函数y=$\sqrt{3}$|x+1|图象上的点,
当x>-1时,y=$\sqrt{3}$x+$\sqrt{3}$,
设P(x,$\sqrt{3}$x+$\sqrt{3}$),如图1,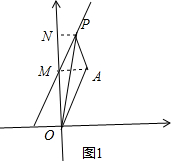
作AM⊥y轴于M,PN⊥y轴于N,
∴S=S梯形AMNP+S△AOM-S△PON
=$\frac{1}{2}$(x+1)($\sqrt{3}$x+$\sqrt{3}$-$\sqrt{3}$)+$\frac{1}{2}$×1×$\sqrt{3}$-$\frac{1}{2}$x($\sqrt{3}$x+$\sqrt{3}$)
=$\frac{\sqrt{3}}{2}$.
当x<-1时,y=-$\sqrt{3}$x-$\sqrt{3}$,
设P(x,-$\sqrt{3}$x-$\sqrt{3}$),如图2,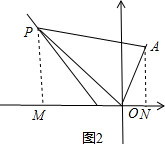
作AN⊥x轴于N,PM⊥x轴于M,
∴S=S梯形ANMP-S△POM-S△PON
=$\frac{1}{2}$(-$\sqrt{3}$x-$\sqrt{3}$+$\sqrt{3}$)(-x+1)-$\frac{1}{2}$×(-x)(-$\sqrt{3}$x-$\sqrt{3}$)-$\frac{1}{2}$×1×$\sqrt{3}$=-$\sqrt{3}$x-$\frac{\sqrt{3}}{2}$(x<-1).
综上,△OAP的面积S与x的函数关系式为:S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{2}(x>-1)}\\{-\sqrt{3}x-\frac{\sqrt{3}}{2}(x<-1)}\end{array}\right.$.
点评 本题考查了一次函数图象上点的坐标特征,分类讨论思想是解决本题的关键.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
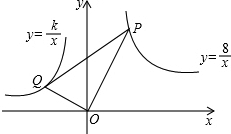 如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.
如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com