练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
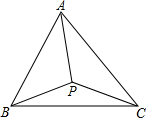
    如图，△ABC内有一点P，且PA=PB=PC，若∠PAB=30°，∠PAC=40°，则∠BPC的大小是（　　）
    A、110°B、130°
    C、120°D、140°
    考点：线段垂直平分线的性质
    专题：
    分析：延长AP到M，根据等边对等角可得∠PAB=∠PBA=30°，∠PAC=∠PCA=40°，再根据三角形内角与外角的性质可得∠BPC的度数．
    解答：解：延长AP到M，
    ∵PA=PB，
    ∴∠PAB=∠PBA=30°，
    ∴∠BPM=60°，
    ∵PA=PC，
    ∴∠PAC=∠PCA=40°，
    ∴∠CPM=80°，
    ∴∠BPC=140°，
    故选：D．
    点评：此题主要考查了等腰三角形的性质，以及三角形的内角与外角的关系，关键是掌握等边对等角．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    如图，以正方形ABCD的一边CD为边向形内作等边三角形CDE，则∠AEB=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如果两个角的两边两两互相垂直，则这两个角（　　）
    A、相等B、互补
    C、相等或互补D、不相等也不互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图是一正方体的展开图，若正方体相对面所表示的数相等，求x，y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，为吉林省农安县城内的一座辽代古塔，为了实现测量古塔外墙底部墙角∠ABC的度数，请你运用所学过的知识设计两种测量方案，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    1
    x2-2x+3
    的最大值是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    抛物线y=ax2+bx+c经过原点，其顶点坐标为（1，
    1
    3
    ），与x轴交于另一点A．
    （1）求此抛物线的解析式；
    （2）将直线y=
    1
    2
    x向下平移与抛物线交于EF两点，若∠EOF=90°，求平移后的直线解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

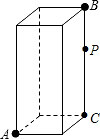    如图，是一长、宽都是3cm，高BC=9cm的长方体纸箱，BC上有一点P，PC=
    2
    3
    BC，一只蚂蚁从点A出发沿纸箱表面爬行到点P的最短距离是（　　）
    A、6
    		2
    cm
    B、3
    		3
    cm
    C、10cm
    D、12cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列事件是必然发生事件的是（　　）
    A、打开电视机，正在转播足球比赛
    B、小麦的亩产量一定为1500千克
    C、在只装有5个红球的袋中摸出1球，是红球
    D、农历十五的晚上一定能看到圆月

    查看答案和解析>>

    同步练习册答案