
ЁОЬтФПЁПФГаЁЧјНЋЩњЛюРЌЛјЗжЮЊПЩЛиЪеЁЂГјгрКЭЦфЫќШ§РрЃЌЗжБ№МЧЮЊaЃЌbЃЌcЃЌВЂЩшжУСЫЯргІЕФРЌЛјЯфЃЌЁАПЩЛиЪеЮяЁБЯфЁЂЁАГјгрРЌЛјЁБЯфКЭЁАЦфЫћРЌЛјЁБЯфЃЌЗжБ№МЧЮЊAЃЌBЃЌC.
ЃЈ1ЃЉФГЬьЃЌаЁУїАбРЌЛјЗжзАдкШ§ИіДќжаЃЌПЩЫћдкЭЖЗХЪБДжаФЃЌУПДќРЌЛјЖМЗХДэСЫЮЛжУЃЈУПИіЯфжажЛЭЖЗХвЛДќЃЉЃЌЧыФугУЛЪїзДЭМЛђСаБэЗЈЧѓаЁУїАбУПДќРЌЛјЖМЗХДэЕФИХТЪЃЛ
ЃЈ2ЃЉЮЊЕїВщОгУёЩњЛюРЌЛјЗжРрЭЖЗХЧщПіЃЌЯжЫцЛњГщШЁСЫИУаЁЧјШ§РрРЌЛјЯфжазм1000ЖжЩњЛюРЌЛјЃЌЪ§ОнЭГМЦШчЯТЃЈЕЅЮЛЃКЖжЃЉЃЛ
A | B | C | |
a | 240 | 30 | 30 |
b | 100 | 400 | 100 |
c | 20 | 20 | 60 |
ЪдЙРМЦЁАПЩЛиЪеЮяЁБЭЖЗХе§ШЗЕФИХТЪ.
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЌ
ЃЌ
ЃЈ2ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§СаБэеЙЪОЫљга6жжЕШПЩФмЕФНсЙћЪ§ЃЌдйевГіАбУПДќРЌЛјЖМЗХДэЕФНсЙћЪ§ЃЌШЛКѓИљОнИХТЪЙЋЪНЧѓНтЃЛ
ЃЈ2ЃЉгУЁАПЩЛиЪеЮяЁБЯфжаПЩЛиЪеЕФРЌЛјСПГ§вдПЩЛиЪеЕФРЌЛјзмСПЃЎ
НтЃКЃЈ1ЃЉгУСаБэЗЈБэЪОГіИїжжЧщПіШчЯТЭМЪОЃК
A | B | C |
a | b | c |
a | c | b |
b | a | c |
b | c | a |
c | a | b |
c | b | a |
ЙВга6жжЕШПЩФмЕФНсЙћЪ§ЃЌЦфжаАбУПДќРЌЛјЖМЗХДэЕФНсЙћЪ§ЮЊ2ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЃЈ2ЃЉвРЬтвтЕУЕУЃК![]() ЃЌ
ЃЌ
ЁрЙРМЦЁАПЩЛиЪеЮяЁБЭЖЗХе§ШЗЕФИХТЪЮЊ![]() ЃЎ
ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП(жаПМЁЄАВЛе)ШчЭМЃЌвбжЊЗДБШР§КЏЪ§yЃН![]() гывЛДЮКЏЪ§yЃНk2xЃЋbЕФЭМЯѓНЛгкA(1ЃЌ8)ЃЌB(Ѓ4ЃЌm)ЃЎ
гывЛДЮКЏЪ§yЃНk2xЃЋbЕФЭМЯѓНЛгкA(1ЃЌ8)ЃЌB(Ѓ4ЃЌm)ЃЎ

(1)Чѓk1ЃЌk2ЃЌbЕФжЕЃЛ
(2)ЧѓЁїAOBЕФУцЛ§ЃЛ
(3)ШєM(x1ЃЌy1)ЃЌN(x2ЃЌy2)ЪЧЗДБШР§КЏЪ§yЃН![]() ЕФЭМЯѓЩЯЕФСНЕуЃЌЧвx1<x2ЃЌy1<y2ЃЌжИГіЕуMЃЌNЮЛгкФФИіЯѓЯоЃЌВЂМђвЊЫЕУїРэгЩЃЎ
ЕФЭМЯѓЩЯЕФСНЕуЃЌЧвx1<x2ЃЌy1<y2ЃЌжИГіЕуMЃЌNЮЛгкФФИіЯѓЯоЃЌВЂМђвЊЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌХзЮяЯпymx22mx3m(mЃО0)ЃЌгыxжсНЛгкAЁЂBСНЕу(AдкBЕФзѓБп)ЃЌгыyжсНЛгкCЕуЃЎMЮЊХзЮяЯпЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНЕуЕФзјБъЃЎ
ЃЈ2ЃЉЕБm=1ЪБЃЌХзЮяЯпBMЖЮгаЕуP(ВЛгыMжиКЯ)ЃЌЪЙЕУSPBCSMBCЃЎЧѓPЕуЕФзјБъЃЎ
ЃЈ3ЃЉЕБm=1ЪБЃЌХзЮяЯпЩЯгаЕуNЃЌЪЙЕУЁЯNCA=2ЁЯBCAЃЎЧѓNЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуCЪЧЁЯAOBЕФЦНЗжЯпЩЯвЛЕуЃЌЕуPЁЂPЁфЗжБ№дкБпOAЁЂOBЩЯЃЎШчЙћвЊЕУЕН OP=OPЁфЃЌашвЊЬэМгвдЯТЬѕМўжаЕФФГвЛИіМДПЩЃЌЧыФуаДГіЫљгаПЩФмЕФНсЙћЕФађКХЮЊЃЈ ЃЉ
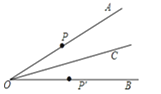
ЂйЁЯOCP=ЁЯOCPЁфЃЛЂкЁЯOPC=ЁЯOPЁфCЃЛЂлPC=PЁфCЃЛЂмPPЁфЁЭOCЃЎ
A.ЂйЂкB.ЂмЂлC.ЂйЂмЂлD.ЂйЂкЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЧѓСНЮЛЪ§ЕФЦНЗНЪБЃЌПЩвдгУЭъШЋЦНЗНЪНМАЁАСаЪњЪНЁБЕФЗНЗЈНјааЫйЫуЃЌЧѓНтЙ§ГЬШчЯТЃЎ
Р§ШчЃКЧѓ322ЃЎ
НтЃКвђЮЊ(3xЃЋ2y)2ЃН9x2ЃЋ4y2ЃЋ12xyЃЌНЋЩЯЪНжаЕШКХгвБпЕФЯЕЪ§ЬюШыЯТУцЕФБэИёжаПЩЕУЃК
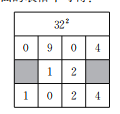
Ыљвд322ЃН1024ЃЎ
(1)ЯТУцЪЧМЮМЮЗТееР§ЬтЧѓ892ЕФвЛВПЗжЙ§ГЬЃЌЧыФуАяЫћЬюШЋБэИёМАзюКѓНсЙћЃЛ
НтЃКвђЮЊ(8xЃЋ9y)2ЃН64x2ЃЋ81y2ЃЋ144xyЃЌНЋЩЯЪНжаЕШКХгвБпЕФЯЕЪ§ЬюШыЯТУцЕФБэИёжаПЩЕУЃК
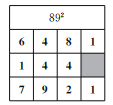
Ыљвд892ЃН ЃЛ
(2)ЗТееР§ЬтЃЌЫйЫу672ЃЛ
(3)чїчїгУЁАСаЪњЪНЁБЕФЗНЗЈМЦЫувЛИіСНЮЛЪ§ЕФЦНЗНЃЌВПЗжЙ§ГЬШчЭМЫљЪОЃЎШєетИіСНЮЛЪ§ЕФИіЮЛЪ§зжЮЊaЃЌдђетИіСНЮЛЪ§ЮЊ (гУКЌaЕФДњЪ§ЪНБэЪО)ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЃЈmЪЧГЃЪ§ЃЉ
ЃЈmЪЧГЃЪ§ЃЉ
ЃЈ1ЃЉжЄУїЃКВЛТлmШЁКЮжЕЪБЃЌИУЖўДЮКЏЪ§ЭМЯѓзмгыxжсгаСНИіНЛЕуЃЛ
ЃЈ2ЃЉШє![]() ЁЂ
ЁЂ![]() ЪЧИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФСНИіВЛЭЌЕуЃЌЧѓЖўДЮКЏЪ§НтЮіЪНКЭmЕФжЕЃЛ
ЪЧИУЖўДЮКЏЪ§ЭМЯѓЩЯЕФСНИіВЛЭЌЕуЃЌЧѓЖўДЮКЏЪ§НтЮіЪНКЭmЕФжЕЃЛ
ЃЈ3ЃЉШє![]() ЃЌ
ЃЌ![]() дкКЏЪ§ЭМЯѓЩЯЃЌЧв
дкКЏЪ§ЭМЯѓЩЯЃЌЧв![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЈНсЙћПЩгУКЌmЕФЪНзгБэЪОЃЉ.
ЕФШЁжЕЗЖЮЇЃЈНсЙћПЩгУКЌmЕФЪНзгБэЪОЃЉ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§y=ax2+bxЉ3aОЙ§ЕуAЃЈЉ1ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉЃЌгыxжсНЛгкСэвЛЕуBЃЌХзЮяЯпЕФЖЅЕуЮЊDЃЎ

ЃЈ1ЃЉЧѓДЫЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉСЌНгDCЁЂBCЁЂDBЃЌЧѓжЄЃКЁїBCDЪЧжБНЧШ§НЧаЮЃЛ
ЃЈ3ЃЉдкЖдГЦжсгвВрЕФХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPDCЮЊЕШбќШ§НЧаЮЃПШєДцдкЃЌЧѓГіЗћКЯЬѕМўЕФЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,вЛЫвТжДЌЮЛгкЕЦЫўPЕФББЦЋЖЋ60ЁуЗНЯђ,гыЕЦЫўPЕФОрРыЮЊ100КЃРяЕФAДІ,Ыќбие§ФЯЗНЯђКНаавЛЖЮЪБМфКѓ,ЕНДяЮЛгкЕЦЫўPЕФФЯЦЋЖЋ37ЁуЗНЯђЩЯЕФBДІ,ЧѓДЫЪБТжДЌЫљдкЕФBДІгыЕЦЫўPЕФОрРы(sin53Ёу=0.8ЃЌsin37Ёу=0.6ЃЌtan53Ёу=1.3ЃЌ![]() НсЙћОЋШЗЕН0.1).
НсЙћОЋШЗЕН0.1).
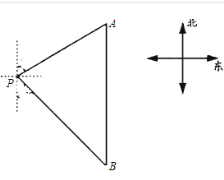
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌDCЪЧЁбOЕФжБОЖЃЌЕуBдкдВЩЯЃЌжБЯпABНЛCDбгГЄЯпгкЕуAЃЌЧвЁЯABD=ЁЯCЃЎ
ЃЈ1ЃЉЧѓжЄЃКABЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШєAB=4cmЃЌAD=2cmЃЌЧѓtanAЕФжЕКЭDBЕФГЄЃЎ
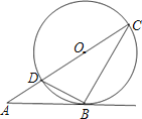
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com