
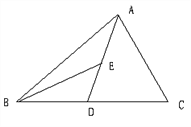
【题目】如图,AD为△ABC的中线,BE为△ABD的中线.
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)作△BED的边BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE 中BD边上的高为多少?
【答案】(1)55°;(2)作图见解析;(3)4.
【解析】试题分析:(1)根据三角形内角与外角的性质解答即可;
(2)过E作BC边的垂线即可;
(3)过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
试题解析:(1)∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°;
(2)过E作BC边的垂线,F为垂足,则EF为所求;
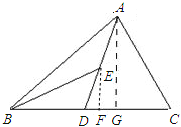
(3)过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴![]() BCAG=40,
BCAG=40,
即![]() ×10AG=40,解得AG=8,
×10AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF=![]() AG=
AG=![]() ×8=4.
×8=4.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
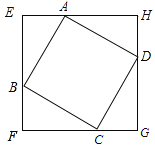
【题目】如图,正方形ABCD的边长为8cm,分别过四个顶点A、B、C、D做四条直线EF、FG、GH、HE,并保证相邻两条直线垂直,相交于E、F、G、H四点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)判断无论如何按照上述要求作图,线段EG、AC的中点是否重合,并说明理由;
(3)判断四边形EFGH的面积有无最大值,若有请写出面积最大值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
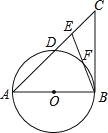
【题目】(2016广西省贺州市第25题)如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育工会为庆祝重阳节活动,在九月份组织退休职工到北京长城、故宫五日游,现联系了青年旅行社、教育旅行社,两家旅行社报价均为3000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:青年旅行社对每位职工七五折优惠;而教育旅行社是免去一位带队领导的费用,其余职工八折优惠.
(1)如果设参加旅游的职工共有m(m>10)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含m的代数式表示,并化简.)
(2)假如这个单位现组织包括带队领导在内的共20名职工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由.
(3)如果计划在九月份外出旅游5天,设最中间一天的日期为m,则这5天的日期之和为 .(用含m的代数式表示,并化简.)
(4)假如这五天的日期之和为70,则他们于九月几号出发.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】能判定一个四边形是菱形的条件是( )
A.对角线互相平分且相等
B.对角线互相垂直且相等
C.对角线互相垂直且对角相等
D.对角线互相垂直,且一条对角线平分一组对角
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com