
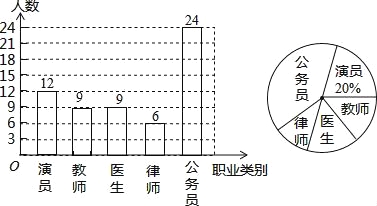
����Ŀ��������ѧ��չ�ԡ�����ϲ����ְҵ��Ϊ����ĵ�����Χ�ơ�����Ա����ʦ��ҽ������ʦ������Ա������ְҵ�У�����ϲ����һ�ࣿ����ѡ��ֻѡһ�ࣩ�������⣬��ȫУ��Χ�������ȡ����ѧ�������ʾ����飬����������������Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ���������ͼ���ṩ����Ϣ�ش��������⣺
��1�����ε��鹲��ȡ�˶�����ѧ����
��2�����ڱ������ѧ���У���ϲ����ʦְҵ������������ȫ����ͳ��ͼ��
��3����������ѧ����1500��ѧ����������Ƹ���ѧ��ϲ����ʦְҵ��ѧ���ж�������

���𰸡���1��60����2��9��ͼ�μ���������3��150.
��������
�����������1������Ա����������Ա��ռ�ٷֱȿɵõ�����ȡ��ѧ����������2����������ȥ�����������ɵó���ʦְҵ���������ٲ�ȫͳ��ͼ����3�����õ���ѧ������ϲ����ʦְҵ��ѧ���ٷֱȿ��������ѧ�е���Ӧ������
�����������1��12��20%=60���𣺹�������60��ѧ������2��60��12��9��6��24=9������ϲ���Ľ�ʦְҵ����Ϊ9�ˣ���ͼ��ʾ��
��3��![]() �������𣺸���ѧ��ϲ����ʦְҵ��ѧ����150����
�������𣺸���ѧ��ϲ����ʦְҵ��ѧ����150����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2017��ij��ҵ���ͳ�����������25Ԫ/ �֡���������������16Ԫ/ �ֵ��շѱ�����֧���ͳ��ͽ�������������5200Ԫ����2018��Ԫ�����շѱ��ϵ�Ϊ���ͳ�����������100Ԫ/ �֣���������������30Ԫ/ �֣�������ҵ2018�괦��������������������2017�����û�б仯����Ҫ��֧������������8800Ԫ��
��1������ҵ2017�괦���IJͳ������ͽ������������ٶ֣�
��2������ҵ�ƻ�2018�꽫�����������������������ٵ�240�֣��ҽ��������������������ͳ�������������3������2018�����ҵ������Ҫ֧���ͳ����������Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����л���ͳ�Ļ���ijУ��֯���꼶1000��ѧ���μӺ�����д����.Ϊ�˽�ѧ��������д���������г�ȡ����ѧ���ijɼ����÷�ȡ������������Ϊ100�֣�����ͳ�Ʒ������õ���������70.5��80.5��Ƶ����50����ռ�ٷֱ�25�����γ����������������Ϊ_____.
���𰸡�200
�����������������50��25%��200��
���Ա��γ������������������200��
�ʴ�Ϊ��200��
�����͡������
��������
13
����Ŀ����֪P1��x1��y1����P2��x2��y2����P3��x3��y3���Ƿ���������![]() ��ͼ���ϵ����㣬��x1��0��x2��x3����y1��y2��y3�Ĵ�С��ϵ��________.
��ͼ���ϵ����㣬��x1��0��x2��x3����y1��y2��y3�Ĵ�С��ϵ��________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ǹ������¶��壺˳����������һ���ı��θ����е����õ��ı��ν��е��ı��Σ�
��1����ͼ1���ı���ABCD�У���E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣮
��֤���е��ı���EFGH��ƽ���ı��Σ�
��2����ͼ2����P���ı���ABCD��һ�㣬������PA=PB��PC=PD����APB=��CPD����E��F��G��H�ֱ�Ϊ��AB��BC��CD��DA���е㣬�����е��ı���EFGH����״����֤����IJ��룻
��3�����ı䣨2���е�������ʹ��APB=��CPD=90�㣬�����������䣬ֱ��д���е��ı���EFGH����״��������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˿�չ�����»����ѧ����ϲ����ͼ�����������һ�γ�������������ͼ��ֳ����ࣺ��������ѧ�����ա���������������˸�Уm��ѧ��(ÿ��ѧ����ѡ��ֻ��ѡ��һ��ͼ��)�������������Ƴ�����������������ͳ��ͼ��

����ͳ��ͼ�ṩ����Ϣ������������⣺
(1)m�� ��n�� ��
(2)����ͳ��ͼ����������������Ӧ�����ε�Բ�ĽǶ����� �ȣ�
(3)�����������Ϣ��ȫ����ͳ��ͼ��
(4)���ݳ�������Ľ����������Ƹ�У1000��ѧ�����ж���ѧ����ϲ��������ͼ�飮
���𰸡� (1)m=50�� n=30����2��72�� (3)��ͼ��������4��300
�������������������1��������������������ռ�İٷֱȼ������m��ֵ���Ӷ��������n��ֵ��
��2����������ͳ��ͼ�е����ݿ������������������Ӧ�����ε�Բ�ĽǶ�����
��3����������������ϲ����ѧ���������Ӷ����Խ�����ͳ��ͼ����������
��4������ͳ��ͼ�е����ݿ��Թ��Ƹ�У600��ѧ�����ж���ѧ����ϲ��������ͼ�飮
���������
�⣺��1��m��5��10%��50��n%��15��50��30%��
�ʴ�Ϊ��50��30��
��2��������ɵã�
������������Ӧ�����ε�Բ�ĽǶ����ǣ�360���![]() ��72����
��72����
�ʴ�Ϊ��72��
��3����ѧ�У�50��10��15��5��20��
��ȫ������ͳ��ͼ��ͼ��ʾ��

��4��������ɵã�
600��![]() ��180��
��180��
����У600��ѧ������180��ѧ����ϲ��������ͼ�飮
�㾦�����⿼������ͳ��ͼ������ͳ��ͼ���������������壬�����Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������������ν�ϵ�˼����
�����͡������
��������
23
����Ŀ�������ǰϦ��С���ĸ�ĸ���������ɸ����Ӻ���Ѽ��(ÿ�����ӵļ۸���ͬ��ÿ����Ѽ���ļ۸���ͬ)����֪���ӵļ۸����Ѽ���ļ۸��1.5Ԫ����35Ԫ�������ӵĸ����뻨20Ԫ������Ѽ���ĸ�����ͬ����������Ѽ���ļ۸���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪һ�κ���y1=kx+b��ͼ���뷴��������![]() ��ͼ����A��B����, �ҵ�A������Ϊ��-2,3������B����������-2,��:
��ͼ����A��B����, �ҵ�A������Ϊ��-2,3������B����������-2,��:
(1)һ�κ����뷴���������Ľ���ʽ;
��2������ͼ��ָ������![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() >
>![]() ����
����![]() Ϊ��ֵʱ��
Ϊ��ֵʱ��![]() ��
��![]()
��3������ͼ��ָ������![]() >3ʱ
>3ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��

���𰸡�������
�������������������1����A��������뷴������������ʽ���m��ֵ����B�����������뷴������������ʽ���B��ĺ����꣬�ٰ�A��B������������һ�κ�������ʽ���k��b��ֵ���ɣ�
��2������A��B�ĺ����꣬���ͼ�ɵó�����
��3�����x��3ʱy2��ֵ��Ȼ����ͼ�ɵó�y2��ȡֵ��Χ��
���������
�⣺��1����A����2��3���ڷ���������y2��![]() ��ͼ���ϣ�
��ͼ���ϣ�
��m����2��3
����6��
�������������Ľ���ʽΪy2��![]() ��
��
��y2����2ʱ��x��3��
��B��3����2����
��A����2��3����B��3����2������y��kx��b�ã�
![]() ��
��
��ã� ![]() ��
��
��һ�κ����Ľ���ʽΪy����x��1��
��2�����ͼ��ɵ�y1��y2ʱ��Ӧ��ͼ���ڵ�A������y�����B֮�䣬
��x����2��0��x��3��
ͬ��y1��y2ʱ��Ӧ��ͼ���ڵ�A��y��֮��͵�B���Ҳ࣬
����2��x��0��x��3��
��3����x��3ʱ��y2����2��
��x��3ʱ������������Ӧ��ͼ���ڵ�B���Ҳಿ�֣�
��Ӧ�ĺ���ֵ��2��y2��0��
�㾦�����⿼����һ�κ����뷴���������Ľ������⣬�ô���ϵ������һ�κ����Ľ���ʽ��֪ʶ�㣬��Ҫ����ѧ���ļ��������۲�ͼ�ε��������������ν��˼�룮
�����͡������
��������
26
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������A(1��0)��B(4��1)��C(4��4)������������![]() (x��0)��ͼ����D����P��һ�κ���y=ax+4-4a(a
(x��0)��ͼ����D����P��һ�κ���y=ax+4-4a(a![]() 0)��ͼ����÷���������ͼ���һ�������㣮
0)��ͼ����÷���������ͼ���һ�������㣮
(1)���������ı���ʽ��
(2)һ�κ���y=ax+4-4a(a![]() 0)��ͼ����һ���㣬ֱ��д��������������.
0)��ͼ����һ���㣬ֱ��д��������������.
(3)����һ�κ���y=ax+4-4a(a![]() 0)����y��x���������Сʱ��ȷ����P�ĺ������ȡֵ��Χ��(����д������)
0)����y��x���������Сʱ��ȷ����P�ĺ������ȡֵ��Χ��(����д������)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���������ABCDE����ijƽ��ֱ������ϵ��������A��B��C��D������ֱ��ǣ�0��a��������3��2������b��m������c��m�������E�������ǣ�������
A.��2����3��
B.��2��3��
C.��3��2��
D.��3����2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���ABCD�ĶԽ���AC��BD���ڵ�O����OE=OF��DF��BE��
��1����֤����BOE�ա�DOF��
��2����֤���ı���DEBF��ƽ���ı��Σ�
��3����OD=OE=OF�����ı���DEBF��ʲô������ı��Σ���֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���״��̷�A�����������ɽ����ϣ��ִ��̷�B�����������ɽ����ϣ�A��B�������������������֮��Ϊ3��2��Ȼ����ص������Դ�A��B�������۵�ƽ����Ϊ����ȫ���������ң������������Ǯ�ˣ�������Ϊ��������
A. �̷�A�ĵ��۴����̷�B�ĵ���
B. �̷�A�ĵ��۵����̷�B�ĵ���
C. �̰�A�ĵ���С���̷�B�ĵ���
D. ��Ǯ���̷�A���̷�B�ĵ�����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com