
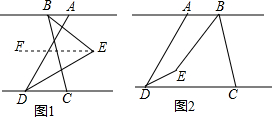
分析 (1)先过点E作EF∥AB,根据平行线的性质即可得出∠BED=∠ABE+∠EDC,再根据角平分线的定义,即可得到$∠BED=\frac{1}{2}∠ABC+\frac{1}{2}∠ADC$,据此可得结果;
(2)过E作EF∥AB,根据平行线的性质即可得出∠ABE=∠BEF,∠FED+∠EDC=180°,再根据角平分线的定义,即可得到∠ABE=$\frac{1}{2}$β,∠EDC=30°,最后根据∠BED=360°-∠BEF-∠DEF进行计算即可.
解答 解:(1)如图1,过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠FED=∠EDC,
∵∠BED=∠BFE+∠FED,
∴∠BED=∠ABE+∠EDC,
∵BE、DE分别是∠ABC、∠ADC的平分线,
∴$∠ABE=\frac{1}{2}∠ABC\;,\;∠EDC=\frac{1}{2}∠ADC$,
∵∠ABC=α,∠ADC=60°,
∴$∠BED=\frac{1}{2}∠ABC+\frac{1}{2}∠ADC$=$\frac{1}{2}α+30°$;
(2)$∠BED=210°-\frac{1}{2}β$,
理由:如图2所示,过E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∴∠ABE=∠BEF,∠FED+∠EDC=180°,
∵∠ABC=β,∠ADC=60°,∠ABC、∠ADC的平分线交于点E,
∴∠ABE=$\frac{1}{2}$β,∠EDC=30°,
∴∠BEF=∠ABE=$\frac{1}{2}$β,∠DEF=180°-∠EDC=150°,
∴∠BED=360°-∠BEF-∠DEF=360°-$\frac{1}{2}$β-150°=210°-$\frac{1}{2}$β.
点评 本题主要考查了平行线的性质以及角平分线的定义的运用,解题时注意:两直线平行,内错角相等.解决问题的关键是作辅助线构造内错角.


科目:初中数学 来源: 题型:填空题
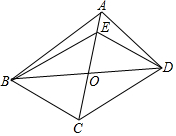 如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).
如图,在四边形ABCD中,对角线AC、BD相交于点O,且OB=OD,点E在线段OA上,连接BE,DE.给出下列条件:①OC=OE;②AB=AD;③BC⊥CD;④∠CBD=∠EBD.请你从中选择两个条件,使四边形BCDE是菱形,并给予证明.你选择的条件是①②(只填写序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.
如图,已知BD是△ABC的角平分线,DE∥AB交BC于E,EF∥AC交AB于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
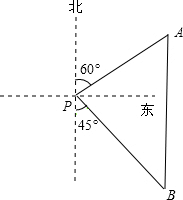 如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)
如图,一艘海轮位于灯塔P的北偏东60°方向,距离灯塔86n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处,此时,B处与灯塔P的距离约为102n mile.(结果取整数,参考数据:$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
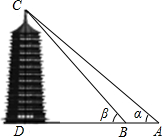 一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.
一数学兴趣小组来到某公园,准备测量一座塔的高度.如图,在A处测得塔顶的仰角为α,在B处测得塔顶的仰角为β,又测量出A、B两点的距离为s米,则塔高为$\frac{tanα•tanβ•s}{tanβ-tanα}$米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{54}$ | B. | $\frac{13}{54}$ | C. | $\frac{1}{13}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com