
 如图,己知双曲线y=
如图,己知双曲线y=| 3 | 16x |
| 3 |
| 16x |
| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
 (1)解:设过A、B两点的直线解析式为y=kx+b(k≠0),
(1)解:设过A、B两点的直线解析式为y=kx+b(k≠0),
|
|
|
|
|
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
(
|
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
| 1 |
| 4 |
|
 (3)①过点D作DM⊥x轴于点M,
(3)①过点D作DM⊥x轴于点M,| 1 |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 3 |
| 3 |
| 3 |
| a |
| 2 |
| a |
| 2 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
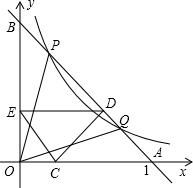 如图,己知双曲线y=
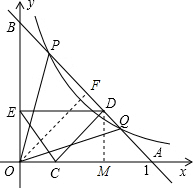
如图,己知双曲线y=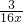 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连接OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连接OP、OQ.查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省苏州市立达中学八年级下学期期末考试数学试卷(带解析) 题型:解答题
如图,己知双曲线y=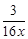 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(1)求△OPQ的面积.
(2)试说明:△OAQ≌△OBP
(3)若C是OA上不与O、A重合的任意一点,CA=a(0<a<1),CD⊥AB于D,DE⊥OB于E.
①a为何值时,CE=AC?
②线段OA上是否存在点C,使CE∥AB?若存在这样的点,请求出点C的坐标:若不存在,请说明理由.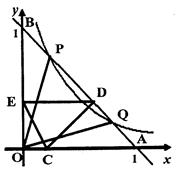
查看答案和解析>>
科目:初中数学 来源:2013届江苏省苏州市八年级下学期期末考试数学试卷(解析版) 题型:解答题
如图,己知双曲线y=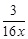 (x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(x>0)与经过点A(1,0)、B(0,1)的直线交于P、Q两点,连结OP、OQ.
(1)求△OPQ的面积.
(2)试说明:△OAQ≌△OBP
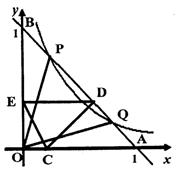
(3)若C是OA上不与O、A重合的任意一点,CA=a(0<a<1),CD⊥AB于D,DE⊥OB于E.
①a为何值时,CE=AC?
②线段OA上是否存在点C,使CE∥AB?若存在这样的点,请求出点C的坐标:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com