
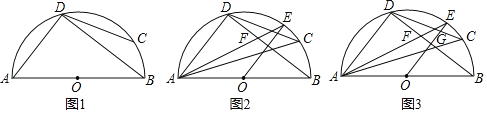
【题目】已知半圆O,点C、D在弧AB上,连接AD、BD、CD,∠BDC+2∠ABD=90°.
(1)如图1,求证:DA=DC;
(2)如图2,作OE⊥BD交半圆O于点E,连接AE交BD于点F,连接AC,求证:∠DFA=∠DAC+∠DAE;
(3)如图3,在(2)的条件下,设AC交BD于点G,FG=1,AG=5,求半圆O的半径.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)连接OD,OC,根据同弧所对的圆心角等于圆周角的2倍得到∠BOC+2∠AOD=180°,再根据∠BOC+∠AOD+∠COD=180°,即可得到∠AOD=∠COD,由此得到结论;
(2)根据垂径定理得到∠DAE=∠EAB,由(1)的结论可得到∠DBA=∠DAC,再根据三角形外角的性质得到结论;
(3)过点A作AM⊥AB,交BD的延长线于点M,连接OD交AC于N,根据等角对等边求出AM=AG=5,根据AB是直径证得∠MAD=∠ABD,再由∠DAE=∠EAB得到∠MAE=∠MFA,从而求出AM=MF=5,根据等腰三角形的三线合一的性质求出DM,根据勾股定理求出AD,再根据三角函数求出AB即可得到半径的长.
证明:(1)如图1,连接OD,OC,
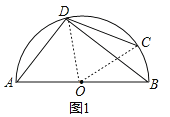
∵∠BOC=2∠BDC,∠AOD=2∠ABD,∠BDC+2∠ABD=90°,
∴∠BOC+2∠AOD=180°,
∵∠BOC+∠AOD+∠COD=180°,
∴∠AOD=∠COD,
∴AD=CD;
(2)如图2,∵OE⊥BD,
∴![]() ,
,
∴∠DAE=∠EAB,
∵AD=CD,
∴∠DAC=∠C,且∠DBA=∠C,
∴∠DBA=∠DAC,
∴∠DFA=∠EAB+∠DBA=∠DAE+∠DAC;
(3)如图2,过点A作AM⊥AB,交BD的延长线于点M,连接OD交AC于N,
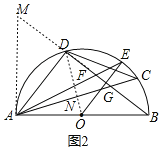
∵OD=OB,
∴∠ABD=∠ODB,
∵AD=CD,
∴OD⊥AC,
∴∠AGD+∠ODB=90°,
∵∠MAB=90°,
∴∠ABD+∠M=90°,
∴∠M=∠AGD,
∴AM=AG=5,
∵AB是直径,
∴∠ADB=90°,
∴∠M+∠MAD=90°,
∴∠MAD=∠ABD,
∴∠MAD+∠DAE=∠ABD+∠EAB,
∴∠MAE=∠MFA,
∴AM=MF=5,
∴MG=MF+FG=6,
∵AD⊥MG,
∴DM=DG=3,
∴DF=DG﹣FG=2,
∴AD=![]() =4,
=4,
∵∠ABD=∠MAD,
∴sin∠ABD=sin∠MAD,
∴![]() ,
,
∴![]() ,
,
∴AB=![]() ,
,
∴OA=![]() ,
,
∴半圆O的半径![]() .
.


科目:初中数学 来源: 题型:
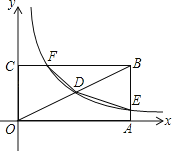
【题目】如图,矩形OABC的顶点A、C分别在x、y轴的正半轴上,点D为对角线OB的中点,反比例函数![]() (x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为_____.
(x>0)在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为1,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
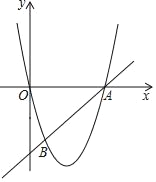
【题目】如图,在平面直角坐标系xOy中,直线AB与抛物线y=ax2+bx交于点A(6,0)和点B(1,﹣5).
(1)求这条抛物线的表达式和直线AB的表达式;
(2)如果点C在直线AB上,且∠BOC的正切值是![]() ,求点C的坐标.
,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
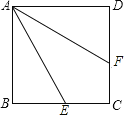
【题目】如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上,线段AE绕点A逆时针旋转后与线段AF重合.若![]() ,则旋转的角度是( )
,则旋转的角度是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你知道为什么任何无限循环小数都可以写成分数形式吗?下面的解答过程会告诉 你原因和方法.
(1)阅读下列材料:
问题:利用一元一次方程将![]() 化成分数.
化成分数.
设 ![]() .
.
由![]() ,可知
,可知 ![]() ,
,
即 ![]() .(请你体会将方程两边都乘以10起到的作用)
.(请你体会将方程两边都乘以10起到的作用)
可解得 ![]() ,即
,即 ![]() .填空:将
.填空:将![]() 写成分数形式为 .
写成分数形式为 .
(2)请仿照上述方法把小数![]() 化成分数,要求写出利用一元一次方程进行解答的过程.
化成分数,要求写出利用一元一次方程进行解答的过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截至北京时间2020年3月22日14时30分,全球新冠肺炎确诊病例达305740例,超过30万,死亡病例累计12762人,将“305740”这个数字用科学记数法表示保留两位有效数字为( )
A.3.05740×105B.3.05×105C.3.0×105D.3.1×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级举行“数学计算能力”比赛,比赛结束后,随机抽查部分学生的成绩,根据抽查结果绘制成如下的统计图表
组别 | 分数x | 频数 |
A | 40≤x<50 | 20 |
B | 50≤x<60 | 30 |
C | 60≤x<70 | 50 |
D | 70≤x<80 | m |
E | 80≤x<90 | 40 |
根据以上信息解答下列问题:
(1)共抽查了 名学生,统计图表中,m= ,请补全直方图;
(2)求扇形统计图中“B组”所对应的圆心角的度数;
(3)若七年级共有800名学生,分数不低于60分为合格,请你估算本次比赛全年级合
格学生的人数

查看答案和解析>>
科目:初中数学 来源: 题型:
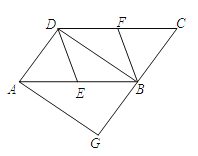
【题目】已知:如图,在![]() 中,
中,![]() 分别在边
分别在边![]() 的中点,
的中点,![]() 是对角线,过点
是对角线,过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() .
.
(1)求证:四边形![]() 是平行四边形;
是平行四边形;
(2)若四边形![]() 是矩形,则四边形
是矩形,则四边形![]() 是什么特殊四边形?并证明你的结论.
是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区为了了解当年春游时学生的个人消费情况,从其中一所学校的初三年级中随机抽取了部分学生春游消费情况进行调查,并将这部分学生的消费额绘制成频率分布直方图.已知从左至右第一组的人数为12名.请根据所给的信息回答:

(1)被抽取调查的学生人数为 名;
(2)从左至右第五组的频率是 ;
(3)假设每组的平均消费额以该组的最小值计算,那么被抽取学生春游的最低平均消费额为 元;
(4)以第(3)小题所求得的最低平均消费额来估计该地区全体学生春游的最低平均消费额,你认为是否合理?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com