
| A. | AM=ME | B. | AM=BE | C. | AM=CN | D. | AM⊥MD |
分析 根据平行四边形的性质证明△EAD≌△FCB,得到∠ADE=∠CBF,证明DE∥BF,根据三角形中位线定理得到AM=MN=CN,得到答案.
解答 证明: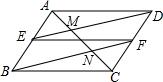 ∵四边形ABCD是平行四边形,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD,∠EAD=∠FCB,
∵E、F分别是边AB、CD的中点,
∴BE=DF,
∴△EAD≌△FCB,
∴∠ADE=∠CBF,
∵AB∥EF∥BC,
∴∠ADE=∠DEF,∠EFB=∠FBC,
∴∠DEF=∠EFB,
∴DE∥BF,
∵AE=EB,CF=FD,
∴AM=MN=CN,
故选:C.
点评 本题考查的是平行四边形的性质和三角形中位线定理,掌握三角形的中位线平行于第三边且等于第三边的一半是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与A重合,折痕为DE,则DE=$\frac{5\sqrt{5}}{4}$.
有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,将△ABC折叠,使点B与A重合,折痕为DE,则DE=$\frac{5\sqrt{5}}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
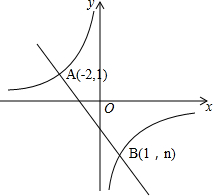 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象相交于A、B两点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com