
 如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).
如图,已知抛物线与x轴交于A(-1,0),B(4,0),与y轴交于C(0,-2).分析 (1)设抛物线的解析式为y=a(x+1)(x-4),然后将(0,-2)代入解析式即可求出a的值;
(2)当△PBH与△AOC相似时,△PBH是直角三角形,由$\frac{OH}{OA}=\frac{OB}{OH}$可知∠AHB=90°,所以求出直线AH的解析式后,联立一次函数与二次函数的解析式后即可求出P的坐标;
(3)设M的坐标为(m,0),由∠BME=∠BDC可知∠EMC=∠MBD,所以△NCM∽△MDB,利用对应边的比相等即可得出CN与m的函数关系式,利用二次函数的性质即可求出m=$\frac{3}{2}$时,CN有最大值,然后再证明△EMB∽△BDM,即可求出E的坐标.
解答 解:(1)∵抛物线与x轴交于A(-1,0),B(4,0),
∴设抛物线的解析式为:y=a(x+1)(x-4),
把(0,-2)代入y=a(x+1)(x-4),
∴a=$\frac{1}{2}$,
∴抛物线的解析式为:y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2;
(2)当△PBH与△AOC相似时,
∴△AOC是直角三角形,
∴△PBH也是直角三角形,
由题意知:H(0,2),
∴OH=2,
∵A(-1,0),B(4,0),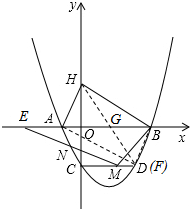
∴OA=1,OB=4,
∴AH=$\sqrt{5}$,BH=2$\sqrt{5}$,
∴AH2+BH2=AB2,
∴∠AHB=90°,
且∠ACO=∠AHO=∠HBA,
∴△AOC∽△AHB,
∴A(-1,0)符合要求,
取AB中点G,则G($\frac{3}{2}$,0),
连接HG并延长至F使GF=HG,连接AF,
则四边形AFBH为矩形,
∴∠HBD=90°,∠BHG=∠GBH=∠AHO=∠ACO,
且F点坐标为(3,-2),
将F(3,-2)代入y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2得,F在抛物线上,
∴点(3,-2)符合要求,
所以符合要求的P点的坐标为(-1,0)和(3,-2).
(3)过点M作MF⊥x轴于点F,
设点E的坐标为(n,0),M的坐标为(m,-2),
∵∠BME=∠BDC,
∴∠EMC+∠BME=∠BDC+∠MBD,
∴∠EMC=∠MBD,
∵CD∥x轴,
∴D的纵坐标为-2,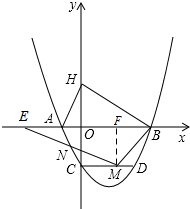
令y=-2代入y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2,
∴x=0或x=3,
∴D(3,-2),
∵B(4,0),
∴由勾股定理可求得:BD=$\sqrt{5}$,
∵M(m,-2),
∴MD=3-m,CM=m(0≤m≤3)
∴由抛物线的对称性可知:∠NCM=∠BDC,
∴△NCM∽△MDB,
∴$\frac{CN}{MD}=\frac{CM}{BD}$,
∴$\frac{CN}{3-m}=\frac{m}{\sqrt{5}}$,
∴CN=$-\frac{\sqrt{5}}{5}({m}^{2}-3m)$=-$\frac{\sqrt{5}}{5}$(m-$\frac{3}{2}$)2+$\frac{9\sqrt{5}}{20}$,
∴当m=$\frac{3}{2}$时,CN可取得最大值,
∴此时M的坐标为($\frac{3}{2}$,-2),
∴MF=2,BF=$\frac{5}{2}$,MD=$\frac{3}{2}$
∴由勾股定理可求得:MB=$\frac{\sqrt{41}}{2}$,
∵E(n,0),
∴EB=4-n,
∵CD∥x轴,
∴∠NMC=∠BEM,∠EBM=∠BMD,
∴△EMB∽△BDM,
∴$\frac{MB}{EB}=\frac{MD}{MB}$,
∴MB2=MD•EB,
∴$\frac{41}{4}$=$\frac{3}{2}$×(4-n),
∴n=-$\frac{17}{6}$,
∴E的坐标为(-$\frac{17}{6}$,0).
点评 本题考查函数的综合问题,涉及待定系数法求解析式,联立解析式求交点坐标,相似三角形判定与性质,二次函数最值等知识,内容较为综合,需要学生灵活运用知识去解决问题.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “投掷一枚骰子,向上的一面显示的点数是1”的概率为$\frac{1}{6}$ | |
| B. | “投掷一枚硬币,正面朝上”属于必然事件 | |
| C. | “为了解河北省中学生课外阅读的情况”应采用普查 | |
| D. | “用长为4cm、6cm、7cm的三条线段围成三角形”属于不可能事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
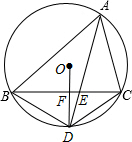 如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )
如图,⊙O是△ABC的外接圆.AD平分∠BAC交⊙O于点D,交BC于点E,连接OD交BC于点F,连接BD,DC.下列五个结论中,正确的有( )| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
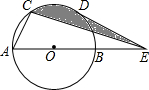 如图所示,在半径为2cm的⊙O中,点C、点D是$\widehat{AB}$的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )
如图所示,在半径为2cm的⊙O中,点C、点D是$\widehat{AB}$的三等分点,点E是直径AB的延长线上一点,连结CE、DE,则图中阴影部分的面积是( )| A. | $\sqrt{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{2π}{3}$-$\sqrt{3}$ | D. | $\frac{2π}{3}$+$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com