
【题目】已知:在平面直角坐标系中,抛物线 y=ax2 -2ax+4(a<0) 交 x 轴于点 A、B,与 y 轴交于点 C,AB=6.

(1)如图 1,求抛物线的解析式;
(2) 如图 2,点 R 为第一象限的抛物线上一点,分别连接 RB、RC,设△RBC 的面积为 s,点 R 的横坐标为 t,求 s 与 t 的函数关系式;
(3)在(2)的条件下,如图 3,点 D 在 x 轴的负半轴上,点 F 在 y 轴的正半轴上,点 E 为 OB 上一点,点 P 为第一象限内一点,连接 PD、EF,PD 交 OC 于点 G,DG=EF,PD⊥EF,连接 PE,∠PEF=2∠PDE,连接 PB、PC,过点R 作 RT⊥OB 于点 T,交 PC 于点 S,若点 P 在 BT 的垂直平分线上,OB-TS=![]() ,求点 R 的坐标.
,求点 R 的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)R(2,4)或R(
;(3)R(2,4)或R(![]() ,
,![]() )
)
【解析】
(1)先求出抛物线的对称轴,再根据A、B关于抛物线对称轴对称和AB的长即可求出A、B的坐标,然后代入解析式即可;
(2)过点R作x轴的垂线,交BC于点M,根据题意可得点R的坐标为![]() ,点M的横坐标为t,然后求出点C的坐标,利用待定系数法求出直线BC的解析式,即可求出点M的坐标,最后利用“铅垂高,水平宽”即可求出结论;
,点M的横坐标为t,然后求出点C的坐标,利用待定系数法求出直线BC的解析式,即可求出点M的坐标,最后利用“铅垂高,水平宽”即可求出结论;
(3)设PG与EF交于点H,连接EG,设R点的坐标为![]() ,则OT=t,根据题意求出点S的坐标,即可求出直线SC的解析式,然后根据全等三角形的判定及性质、垂直平分线的判定、三线合一证出OP平分∠EOG,可得点P的横纵坐标相等,再结合已知条件即可求出点P的坐标,代入直线SC的解析式即可求出t,从而求出点R的坐标.
,则OT=t,根据题意求出点S的坐标,即可求出直线SC的解析式,然后根据全等三角形的判定及性质、垂直平分线的判定、三线合一证出OP平分∠EOG,可得点P的横纵坐标相等,再结合已知条件即可求出点P的坐标,代入直线SC的解析式即可求出t,从而求出点R的坐标.
解:(1)抛物线 y=ax2 -2ax+4(a<0)的对称轴为x=![]()
∵AB=6,A、B关于x=1对称
∴点A的横坐标为1-![]() =-2,点B的横坐标为1+
=-2,点B的横坐标为1+![]() =4
=4
∴点A的坐标为(-2,0),点B的坐标为(4,0)
将点A的坐标代入y=ax2 -2ax+4中,得
0=4a+4a+4
解得:a=![]()
∴抛物线的解析式为![]() ;
;
(2)过点R作x轴的垂线,交BC于点M
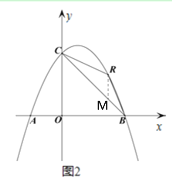
∵点 R 的横坐标为 t
∴点R的坐标为![]() ,点M的横坐标为t
,点M的横坐标为t
将x=0代入![]() 中,解得y=4
中,解得y=4
∴点C的坐标为(0,4)
设直线BC的解析式为y=kx+b
将点B、C的坐标代入,得
![]()
解得:![]()
∴直线BC的解析式为y=-x+4
∴点M的坐标为(t,-t+4)
∴RM=![]()
∴s=![]() RM·(xB-xC)=
RM·(xB-xC)=![]()
![]() ·(4-0)=
·(4-0)=![]()
(3)设PG与EF交于点H,连接EG
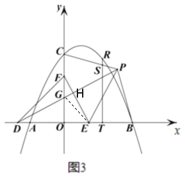
设R点的坐标为![]() ,则OT=t
,则OT=t
∵OB-TS=![]() ,OB=4
,OB=4
∴TS=![]()
∴点S的坐标为(t,![]() )
)
设直线SC的解析式为:y=mx+n
将S、C的坐标代入,得
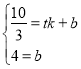
解得: 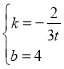
∴直线SC的解析式为![]()
∵∠DOG=∠FOE=∠DHE=90°
∴∠ODG+∠HEO=90°,∠OFE+∠HEO=90°
∴∠ODG=∠OFE
∵DG=FE
∴△ODG≌△OFE
∴OG=OE,
∴点O在GE的中垂线上,△OGE为等腰直角三角形
∴∠GEO=∠OGE=45°
∴∠PGE=∠GEO+∠PDE=45°+∠PDE,∠FEG=∠OGE-∠OFE=45°-∠PDE
∵∠PEF=2∠PDE
∴∠PEG=∠PEF+∠FEG=2∠PDE+45°-∠PDE=45°+∠PDE
∴∠PGE=∠PEG
∴PG=PE
∴点P在EG的中垂线上
∴OP垂直平分EG
∴OP平分∠EOG
∴点P的横、纵坐标相等
∵点 P 在 BT 的垂直平分线上
∴点P的坐标为(![]() )
)
将点P的坐标代入直线SC的解析式中,得
![]()
解得:![]()
经检验:![]() 均为原方程的解
均为原方程的解
当t=2时,点R的坐标为(2,4);
当t=![]() 时,点R的坐标为(
时,点R的坐标为(![]() ,
,![]() )
)
综上所述:R(2,4)或R(![]() ,
,![]() )
)


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
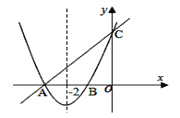
【题目】已知:抛物线与直线y=x+3分别交于x轴和y轴上同一点,交点分别是点A和点C,且抛物线的对称轴为直线x=-2.
(1)求出抛物线与x轴的两个交点A、B的坐标.
(2)试确定抛物线的解析式.
(3)观察图象,请直接写出二次函数值小于一次函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用
,在地面上有两根等长的立柱AB,CD,它们之间悬挂了一根抛物线形状的绳子,按照图中的直角坐标系,这条绳子可以用![]() 表示
表示
![]() 求这条绳子最低点离地面的距离;
求这条绳子最低点离地面的距离;
![]() 现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑
现由于实际需要,要在两根立柱之间再加一根立柱EF对绳子进行支撑![]() 如图
如图![]() ,已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.
,已知立柱EF到AB距离为3m,两旁的绳子也是抛物线形状,且立柱EF左侧绳子的最低点到EF的距离为1m,到地面的距离为1.8m,求立柱EF的长.
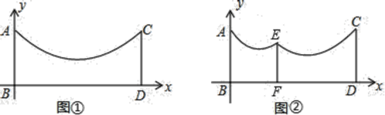
查看答案和解析>>
科目:初中数学 来源: 题型:
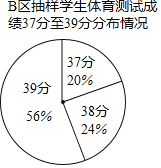
【题目】为了调查A、B两个区的初三学生体育测试成绩,从两个区各随机抽取了1000名学生的成绩(满分:40分,个人成绩四舍五入向上取整数)
A区抽样学生体育测试成绩的平均分、中位数、众数如下:
平均分 | 中位数 | 众数 |
37 | 36 | 37 |
B区抽样学生体育测试成绩的分布如下:
成绩 | 28≤x<31 | 31≤x<34 | 34≤x<37 | 37≤x<40 | 40(满分) |
人数 | 60 | 80 | 140 | m | 220 |
请根据以上信息回答下列问题
(1)m= ;
(2)在两区抽样的学生中,体育测试成绩为37分的学生,在 (填“A”或“B”)区被抽样学生中排名更靠前,理由是 ;
(3)如果B区有10000名学生参加此次体育测试,估计成绩不低于34分的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在 10×6 的正方形网格中,每个小正方形的边长均为 1,线段 AB 的端点 A、B 均在小正方形的顶点上.

(1)在图中画出以 AB 为一腰的等腰△ABC,点 C 在小正方形顶点上,△ABC 为钝角三角形,且△ABC 的面积为![]() ;
;
(2)在图中画出以 AB 为斜边的直角三角形 ABD, 点 D在小正方形的顶点上,且 AD>BD;
(3)连接 CD,请你直接写出线段 CD 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
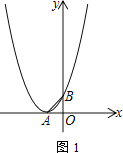
【题目】如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0,其中正确的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线顶点A在x轴负半轴上,与y轴交于点B,OB=1,△OAB为等腰直角三角形
(1)求抛物线的解析式
(2)若点C在抛物线上,若△ABC为直角三角形,求点C的坐标
(3)已知直线DE过点(-1,-4),交抛物线于点D、E,过D作DF∥x轴,交抛物线于点F,求证:直线EF经过一个定点,并求定点的坐标

查看答案和解析>>
科目:初中数学 来源: 题型:
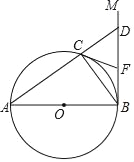
【题目】如图,AB为⊙O的直径,直线BM⊥AB于点B,点C在⊙O上,分别连接BC,AC,且AC的延长线交BM于点D,CF为⊙O的切线交BM于点F.
(1)求证:CF=DF;
(2)连接OF,若AB=10,BC=6,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
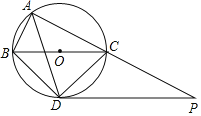
【题目】如图,⊙O是△ABC的外接圆,点O在BC边上,∠BAC的平分线交⊙O于点D,连接BD、CD,过点D作BC的平行线与AC的延长线相交于点P.
(1)求证:PD是⊙O的切线;
(2)求证:△ABD∽△DCP;
(3)当AB=5cm,AC=12cm时,求线段PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com