
已知 是某直角三角形内角中较大的锐角,
是某直角三角形内角中较大的锐角, 是某五边形的外角中的最大角,甲、乙、丙、丁
是某五边形的外角中的最大角,甲、乙、丙、丁
计算 的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )
的结果依次为10°、15°、30°、35°,其中有正确的结果,则计算正确的是( )
A.甲 B.乙 C.丙 D.丁
科目:初中数学 来源: 题型:阅读理解
| |x2-x1|2+|y2-y1|2 |
| (x-0)2+(y-0)2 |
 原点,半径为r的圆的方程.
原点,半径为r的圆的方程.查看答案和解析>>
科目:初中数学 来源: 题型:
 学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.
学习了勾股定理的逆定理,我们知道:在一个三角形中,如果两边的平方和等于第三边的平方,那么这个三角形为直角三角形.类似地,我们定义:对于任意的三角形,设其三个角的度数分别为x°、y°和z°,若满足x2+y2=z2,则称这个三角形为勾股三角形.| 6 |
| 3 |
查看答案和解析>>
科目:初中数学 来源:安徽省期末题 题型:解答题
 ,
, 是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。
是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。 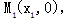
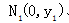
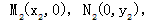 直线AN1与BM2交于Q点。
直线AN1与BM2交于Q点。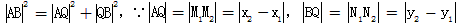
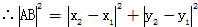
 之间的距离公式:
之间的距离公式: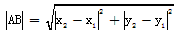
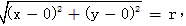 整理得:x2+y2=r2。我们称此式为圆心在原点,半径为r的圆的方程。
整理得:x2+y2=r2。我们称此式为圆心在原点,半径为r的圆的方程。 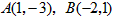 之间的距离;
之间的距离;查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解
阅读下列材料后回答问题:
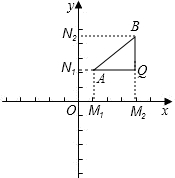
在平面直角坐标系中,已知x轴上的两点A(X1,0),B(X2,0)的距离记作![]() ,如果
,如果![]() 是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。
是平面上任意两点,我们可以通过构造直角三角形来求A、B间的距离。
如图,过A、B两点分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别记作![]() ,
,![]() 、
、![]() ,
,![]() ,直线AN1与BM2交于Q点。
,直线AN1与BM2交于Q点。
在Rt△ABQ中,![]() ,∵
,∵![]() ,
,![]()
∴![]()
由此得任意两点![]() 之间的距离公式:
之间的距离公式:![]()
如果某圆的圆心为(0,0),半径为r。设P(x,y)是圆上任一点,根据“圆上任一点到定点(圆心)的距离都等于定长(半径)”,我们不难得到![]() ,即:
,即:![]() , 整理得:
, 整理得:![]() 。我们称此式为圆心在原点,半径为r的圆的方程。
。我们称此式为圆心在原点,半径为r的圆的方程。
(1)直接应用平面内两点间距离公式,求点![]() 之间的距离;
之间的距离;
(2)如果圆心在点P(2,3),半径为3,求此圆的方程。
(3)方程![]() 是否是圆的方程?如果是,求出圆心坐标与半径。
是否是圆的方程?如果是,求出圆心坐标与半径。
查看答案和解析>>
科目:初中数学 来源:2009-2010学年安徽省亳州市蒙城县涡南片19校联考九年级(上)期末数学试卷(解析版) 题型:解答题
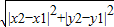
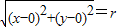 ,整理得:x2+y2=r2.我们称此式为圆心在原点,半径为r的圆的方程.
,整理得:x2+y2=r2.我们称此式为圆心在原点,半径为r的圆的方程.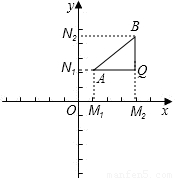
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com