
ЁОЬтФПЁПЖўДЮКЏЪ§y=![]() +bx+cЃЈaЃО0ЃЉЕФЖЅЕуЮЊPЃЌЦфЭМЯѓгыxжсгаСНИіНЛЕуAЃЈЉmЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌНЛyжсгкЕуCЃЈ0ЃЌЉ3am+6aЃЉЃЌвдЯТЫЕЗЈЃКЂйm=3ЃЛЂкЕБЁЯAPB=120ЁуЪБЃЌa=
+bx+cЃЈaЃО0ЃЉЕФЖЅЕуЮЊPЃЌЦфЭМЯѓгыxжсгаСНИіНЛЕуAЃЈЉmЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌНЛyжсгкЕуCЃЈ0ЃЌЉ3am+6aЃЉЃЌвдЯТЫЕЗЈЃКЂйm=3ЃЛЂкЕБЁЯAPB=120ЁуЪБЃЌa=![]() ЃЛЂлЕБЁЯAPB=120ЁуЪБЃЌХзЮяЯпЩЯДцдкЕуMЃЈMгыPВЛжиКЯЃЉЃЌЪЙЕУЁїABMЪЧЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮЃЛЂмХзЮяЯпЩЯДцдкЕуNЃЌЕБЁїABNЮЊжБНЧШ§НЧаЮЪБЃЌгаaЁн
ЃЛЂлЕБЁЯAPB=120ЁуЪБЃЌХзЮяЯпЩЯДцдкЕуMЃЈMгыPВЛжиКЯЃЉЃЌЪЙЕУЁїABMЪЧЖЅНЧЮЊ120ЁуЕФЕШбќШ§НЧаЮЃЛЂмХзЮяЯпЩЯДцдкЕуNЃЌЕБЁїABNЮЊжБНЧШ§НЧаЮЪБЃЌгаaЁн![]() .е§ШЗЕФЪЧЃЈ ЃЉ.
.е§ШЗЕФЪЧЃЈ ЃЉ.
AЃЎЂйЂк BЃЎЂлЂм CЃЎЂйЂкЂл DЃЎЂйЂкЂлЂм
ЁОД№АИЁПD.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЂйАбAЁЂBСНЕуЕФзјБъЗжБ№ДњШыХзЮяЯпЕФНтЮіЪНЕУЕН![]() ЂйЪНКЭa+b+c=0ЂкЪНЃЌНЋСНЪНЯрМѕМДПЩЕУЕНm=
ЂйЪНКЭa+b+c=0ЂкЪНЃЌНЋСНЪНЯрМѕМДПЩЕУЕНm=![]() ЃЌМДПЩЕУЕНCЃЈ0ЃЌ3aЉ3bЃЉЃЌДгЖјЕУЕНc=3aЉ3bЃЌДњШыЂкЪНПЩЕУb=2aЃЌЫљвдm=
ЃЌМДПЩЕУЕНCЃЈ0ЃЌ3aЉ3bЃЉЃЌДгЖјЕУЕНc=3aЉ3bЃЌДњШыЂкЪНПЩЕУb=2aЃЌЫљвдm=![]() =3ЃЌЙЪЂйе§ШЗЃЛ
=3ЃЌЙЪЂйе§ШЗЃЛ
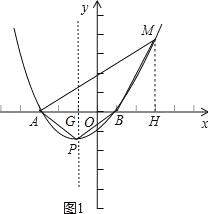
ЂкЁпm=3ЃЌЁпAЃЈЉ3ЃЌ0ЃЉЃЌЁрХзЮяЯпЕФНтЮіЪНПЩЩшЮЊy=aЃЈx+3ЃЉЃЈxЉ1ЃЉЃЌПЩЕУЖЅЕуPЕФзјБъЮЊЃЈЉ1ЃЌЉ4aЃЉЃЎИљОнЖдГЦадПЩЕУPA=PBЃЌЁрЁЯPAB=ЁЯPBA=30ЁуЃЎЩшХзЮяЯпЕФЖдГЦжсгыxжсЕФНЛЕуЮЊGЃЌдђгаPGЁЭxжсЃЌЁрPG=AGtanЁЯPAG=2ЁС![]() =
=![]() ЃЌЁр4a=
ЃЌЁр4a=![]() ЃЌЁрa=
ЃЌЁрa=![]() ЃЌЙЪЂке§ШЗЃЛ
ЃЌЙЪЂке§ШЗЃЛ
ЂлдкЕквЛЯѓЯоФкзїЁЯMBA=120ЁуЃЌЧвТњзуBM=BAЃЌЙ§ЕуMзїMHЁЭxжсгкHЃЌШчЭМ1ЃЌдкRtЁїMHBжаЃЌЁЯMBH=60ЁуЃЌдђгаMH=4sin60Ёу=4ЁС![]() =
=![]() ЃЌBH=4cos60Ёу=4ЁС
ЃЌBH=4cos60Ёу=4ЁС![]() =2ЃЌЁрЕуMЕФзјБъЮЊЃЈ3ЃЌ
=2ЃЌЁрЕуMЕФзјБъЮЊЃЈ3ЃЌ![]() ЃЉЃЌЕБx=3ЪБЃЌy=
ЃЉЃЌЕБx=3ЪБЃЌy=![]() ЃЈ3+3ЃЉЃЈ3Љ1ЃЉ=
ЃЈ3+3ЃЉЃЈ3Љ1ЃЉ=![]() ЃЌЁрЕуMдкХзЮяЯпЩЯЃЌЙЪЂле§ШЗЃЛ
ЃЌЁрЕуMдкХзЮяЯпЩЯЃЌЙЪЂле§ШЗЃЛ
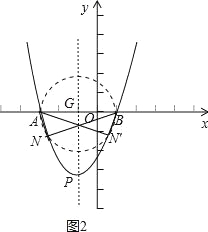
ЂмЁпЕуNдкХзЮяЯпЩЯЃЌЁрЁЯABNЁй90ЁуЃЌЁЯBANЁй90ЁуЃЎЕБЁїABNЮЊжБНЧШ§НЧаЮЪБЃЌЁЯANB=90ЁуЃЌДЫЪБЕуNдквдABЮЊжБОЖЕФЁбGЩЯЃЌвђЖјЕуNдкЁбGгыХзЮяЯпЕФНЛЕуДІЃЌвЊЪЙЕуNДцдкЃЌЕуPБиаыдкЁбGЩЯЛђЁбGЭтЃЌШчЭМ2ЃЌдђгаPGЁн2ЃЌМД4aЁн2ЃЌвВМДaЁн![]() ЃЌЙЪЂме§ШЗЃЎ
ЃЌЙЪЂме§ШЗЃЎ
ЙЪбЁЃКDЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЮЊЖЋУївЛжааТаЃЧјЗжВМЭМЕФвЛВПЗжЃЌЗНИёжНжаУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛЕФе§ЗНаЮЃЌШєНЬбЇТЅЕФзјБъЮЊAЃЈ1ЃЌ2ЃЉЃЌЭМЪщЙнЕФЮЛжУзјБъЮЊBЃЈ-2ЃЌ-1ЃЉЃЌНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉдкЭМжаевЕНзјБъЯЕжаЕФдЕуЃЌВЂНЈСЂжБНЧзјБъЯЕЃЛ
ЃЈ2ЃЉШєЬхг§ЙнЕФзјБъЮЊCЃЈ1ЃЌ-3ЃЉЃЌЪГЬУзјБъЮЊDЃЈ2ЃЌ0ЃЉЃЌЧыдкЭМжаБъГіЬхг§ЙнКЭЪГЬУЕФЮЛжУЃЛ
ЃЈ3ЃЉЫГДЮСЌНгНЬбЇТЅЁЂЭМЪщЙнЁЂЬхг§ЙнЁЂЪГЬУЕУЕНЫФБпаЮABCDЃЌЧѓЫФБпаЮABCDЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
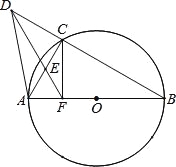
ЁОЬтФПЁПвбжЊABЪЧАыОЖЮЊ1ЕФдВOжБОЖЃЌCЪЧдВЩЯвЛЕуЃЌDЪЧBCбгГЄЯпЩЯвЛЕуЃЌЙ§ЕуDЕФжБЯпНЛACгкEЕуЃЌЧвЁїAEFЮЊЕШБпШ§НЧаЮ
ЃЈ1ЃЉЧѓжЄЃКЁїDFBЪЧЕШбќШ§НЧаЮЃЛ
ЃЈ2ЃЉШєDA=![]() AFЃЌЧѓжЄЃКCFЁЭABЃЎ
AFЃЌЧѓжЄЃКCFЁЭABЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСадЫЫуе§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A.ЃЈxmЃЉ2ЃНxm+2B.ЃЈЉ2x2yЃЉ3ЃНЉ8x5y3
C.x6ЁТx3ЃНx2D.x3x2ЃНx5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
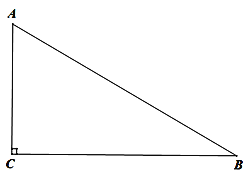
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯACB=90Ёу,ЁЯAЃОЁЯB.
ЃЈ1ЃЉРћгУГпЙцзїЭМдкBCБпЩЯеввЛЕуPЃЌЪЙЕУЕуPЕНABЕФОрРыЕШгкPCЕФГЄЖШЃЈВЛаДзїЗЈЃЌБЃСєзїЭМКлМЃЃЉЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЉЕФЬѕМўЯТЃЌШчЙћЕуPЧЁКУгждкЯпЖЮABЕФДЙжБЦНЗжЯпЩЯ,ЧѓЁЯBЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫужае§ШЗЕФЪЧЃЈ ЃЉ
A.x3x2=2x6
B.ЃЈЉ3x3ЃЉ2=Љ6x6
C.ЃЈx3ЃЉ2=x5
D.x6ЁТx2=x4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСавРДЮХХСаЕФвЛСаЪ§ЃЎЧыНгзХаДГіКѓУцЕФ3ИіЪ§КЭЕк10ИіЪ§ЃЎ
Ђй 1ЃЌ-2ЃЌ1ЃЌ-2ЃЌ1ЃЌ-2ЃЌ ЃЌ ЃЌ ЃЛ ЃЎ
Ђк1ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌ ЃЌ ЃЌ ЃЛ ЃЎ
ЃЌ ЃЌ ЃЌ ЃЛ ЃЎ
Ђл-2ЃЌ4ЃЌ-6ЃЌ8ЃЌ-10ЃЌ ЃЌ ЃЌ ЃЛ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЗНГЬx2+mx+3=0ЕФвЛИіИљЪЧ1ЃЌдђЫќЕФСэвЛИіИљЪЧ ЃЌ mЕФжЕЪЧЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЁЂаЁССЁЂаЁЗМКЭСНИіФАЩњШЫМзЁЂввЭЌдкШчЭМЫљЪОЕФЕиЯТГЕПтЕШЕчЬнЃЌвбжЊСНИіФАЩњШЫЕН1жС4ВуЕФШЮвтвЛВуГіЕчЬнЃЌВЂЩшМздкaВуГіЕчЬнЃЌввдкbВуГіЕчЬнЃЎ
ЃЈ1ЃЉЧыФугУЛЪїзДЭМЛђСаБэЗЈЧѓГіМзЁЂввЖўШЫдкЭЌвЛВуТЅГіЕчЬнЕФИХТЪЃЛ
ЃЈ2ЃЉаЁССКЭаЁЗМДђЖФЫЕЃКЁАШєМзЁЂввдкЭЌвЛВуЛђЯрСкТЅВуГіЕчЬнЃЌдђаЁССЪЄЃЌЗёдђаЁЗМЪЄЁБЃЎИУгЮЯЗЪЧЗёЙЋЦНЃПЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com