
【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行附近的B地,已知B地位于A地的北偏东67°方向,距离A地520km,C地位于B地南偏西30°方向,若要打通穿山隧道建高铁,求线段AC的长(结果保留整数)(参考数据:![]() ≈1.73,sin67°≈
≈1.73,sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() )
)

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
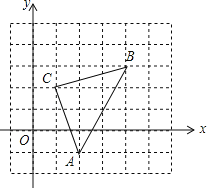
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中,C点坐标为(1,2).
(1)填空:点A的坐标是 ,点B的坐标是 ;
(2)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到△A′B′C′.请写出△A′B′C′的三个顶点坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 在第一象限的图象上有A、B两点,过点B作
在第一象限的图象上有A、B两点,过点B作![]() 轴于点C,现有一动点P从点A出发,沿
轴于点C,现有一动点P从点A出发,沿![]() 匀速运动,终点为C,在点P的运动过程中,分别过点P作
匀速运动,终点为C,在点P的运动过程中,分别过点P作![]() 轴于点M,
轴于点M,![]() 轴于点N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是
轴于点N,设四边形OMPN的面积为S,P点运动的时间为t,则S关于t的函数图象大致是![]()
![]()

A.  B.
B. 
C.  D.
D. 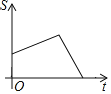
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形![]() 不是等腰三角形
不是等腰三角形![]() 一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
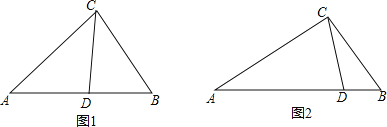
![]() 如图1,在
如图1,在![]() 中,CD为角平分线,
中,CD为角平分线,![]() ,
,![]() ,求证:CD为
,求证:CD为![]() 的完美分割线.
的完美分割线.
![]() 在
在![]() 中,
中,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 为等腰三角形,求
为等腰三角形,求![]() 的度数.
的度数.
![]() 如图2,
如图2,![]() 中,
中,![]() ,
,![]() ,CD是
,CD是![]() 的完美分割线,且
的完美分割线,且![]() 是以CD为底边的等腰三角形,求完美分割线CD的长.
是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△AEB和Rt△AFC中,BE与AC相交于点M,与CF相交于点D,AB与CF相交于N,∠E=∠F=90°,∠EAC=∠FAB,AE=AF.给出下列结论:①∠B=∠C;②CD=DN;③BE=CF;④△ACN≌△ABM.其中正确的结论是( )

A. ①③④ B. ②③④ C. ①②③ D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB交CD于点O,OE平分∠BOD,OF平分∠COB,∠AOD:∠BOE=5:2,则∠AOF等于( )

A. 140° B. 130° C. 120° D. 110°
查看答案和解析>>
科目:初中数学 来源: 题型:
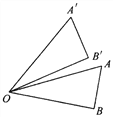
【题目】如图,Rt△AOB绕着一点旋转到△A′OB′的位置,可以看到点A旋转到点A′,OA旋转到OA′,∠AOB旋转到∠A′OB′,这些都是互相对应的点、线段和角.已知∠AOB=30°,∠AOB′=10°,那么点B的对应点是点______;线段OB的对应线段是线段_____;∠A的对应角是______;旋转中心是点_______;旋转的角度是______度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,AD是△ABC的角平分线,DE⊥AB,垂足为点E,AE=BE.
(1)猜想:∠B的度数,并证明你的猜想.
(2)如果AC=3cm,CD=2cm,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y = 2x2 -4x -6.
(1)用配方法将y = 2x2 -4x -6化成y = a (x - h) 2 + k的形式;并写出对称轴和顶点坐标。
(2)在平面直角坐标系中,画出这个二次函数的图象;
(3)当x取何值时,y随x的增大而减少?
(4)当x取何值是,![]() ,y<0,
,y<0,
(5)当![]() 时,求y的取值范围;
时,求y的取值范围;
(6)求函数图像与两坐标轴交点所围成的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com