
【题目】某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇,如表是近两周的销售情况:(进价、售价均保持不变,利润=销售收入﹣进货成本)
销售时段 | 销售数量 | 销售收入 | |
A种型号 | 种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
【答案】(1)A、B两种型号电风扇的销售单价分别为200元、150元;(2)超市最多采购A种型号电风扇37台时,采购金额不多于7500元;(3)能,方案有两种:当a=36时,采购A种型号的电风扇36台,B种型号的电风扇14台;当a=37时,采购A种型号的电风扇37台,B种型号的电风扇13台.
【解析】
(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得得到方程,求解即可得到答案.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
由题意得160a+120(30﹣a)≤7500,求解即可得到答案.
(3)根据题意得:(200﹣160)a+(150﹣120)(50﹣a)>1850,解得:a>35,
由于a≤37![]() ,且a应为整数,所以在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种.
,且a应为整数,所以在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种.
解:(1)设A、B两种型号电风扇的销售单价分别为x元、y元,
依题意得:![]() ,解得:
,解得:![]() ,
,
答:A、B两种型号电风扇的销售单价分别为200元、150元.
(2)设采购A种型号电风扇a台,则采购B种型号电风扇(50﹣a)台.
依题意得:160a+120(30﹣a)≤7500,解得:a≤37![]() .
.
答:超市最多采购A种型号电风扇37台时,采购金额不多于7500元.
(3)根据题意得:(200﹣160)a+(150﹣120)(50﹣a)>1850,解得:a>35,
∵a≤37![]() ,且a应为整数,
,且a应为整数,
∴在(2)的条件下超市能实现利润超过1850元的目标.相应方案有两种:
当a=36时,采购A种型号的电风扇36台,B种型号的电风扇14台;
当a=37时,采购A种型号的电风扇37台,B种型号的电风扇13台.


科目:初中数学 来源: 题型:
【题目】已知数轴上两点![]() 所表示的数分别为
所表示的数分别为![]() 和
和![]() ,且满足
,且满足![]() ,
,![]() 为原点.
为原点.
(1)试求![]() 和
和![]() 的值;
的值;
(2)点![]() 从
从![]() 点出发向右运动,经过3秒后点
点出发向右运动,经过3秒后点![]() 到
到![]() 点的距离是点
点的距离是点![]() 到
到![]() 点距离的3倍,求点
点距离的3倍,求点![]() 的运动速度?
的运动速度?
(3)点![]() 以一个单位每秒的速度从点
以一个单位每秒的速度从点![]() 向右运动,同时点
向右运动,同时点![]() 从点
从点![]() 出发以5个单位每秒的速度向左运动,点
出发以5个单位每秒的速度向左运动,点![]() 从点
从点![]() 出发,以20个单位每秒的速度向右运动.在运动过程中,
出发,以20个单位每秒的速度向右运动.在运动过程中,![]() 分别为
分别为![]() 的中点,问
的中点,问![]() 的值是否发生变化,请说明理由.
的值是否发生变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,![]() 、
、![]() 、
、![]() 分别为数轴上的三个点,
分别为数轴上的三个点,![]() 点对应的数为60,
点对应的数为60,![]() 点在
点在![]() 点的左侧,并且与
点的左侧,并且与![]() 点的距离为30,
点的距离为30,![]() 点在
点在![]() 点左侧,
点左侧,![]() 点到
点到![]() 距离是
距离是![]() 点到
点到![]() 点距离的4倍.
点距离的4倍.
![]()
(1)求出数轴上![]() 点对应的数及
点对应的数及![]() 的距离.
的距离.
(2)点![]() 从
从![]() 点出发,以3单位/秒的速度项终点
点出发,以3单位/秒的速度项终点![]() 运动,运动时间为
运动,运动时间为![]() 秒.
秒.
①点![]() 点在
点在![]() 之间运动时,则
之间运动时,则![]() _______.(用含
_______.(用含![]() 的代数式表示)
的代数式表示)
②![]() 点在
点在![]() 点向
点向![]() 点运动过程中,何时
点运动过程中,何时![]() 、
、![]() 、
、![]() 三点中其中一个点是另外两个点的中点?求出相应的时间
三点中其中一个点是另外两个点的中点?求出相应的时间![]() .
.
③当![]() 点运动到
点运动到![]() 点时,另一点
点时,另一点![]() 以5单位/秒速度从
以5单位/秒速度从![]() 点出发,也向
点出发,也向![]() 点运动,点
点运动,点![]() 到达
到达![]() 点后立即原速返回到
点后立即原速返回到![]() 点,那么
点,那么![]() 点在往返过程中与
点在往返过程中与![]() 点相遇几次?直接写出相遇是
点相遇几次?直接写出相遇是![]() 点在数轴上对应的数.
点在数轴上对应的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是直线AC外的一点,点D,E分别是AC,CB两边上的点,点P关于CA的对称点P1恰好落在线段ED上,P点关于CB的对称点P2落在ED的延长线上,若PE=2.5,PD=3,ED=4,则线段P1P2的长为_____.
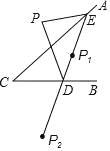
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年端午节,在大明湖举行第七届会民健身运动会龙舟赛中,甲、乙两队在500米的赛道上,所划行的路程y(m)时间x(min)之间的关系如图所示,下列说法中正确的有( )
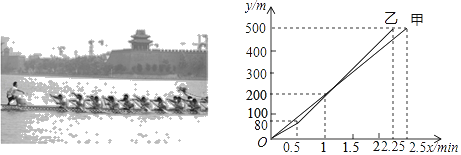
①乙队比甲队提前0.25min到达终点
②当乙队划行110m时,仍在甲队后面;
③当乙队划行200m时,已经超过甲队
④0.5min后,乙队比甲队每分钟快40m
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数1个1,2个![]() ,3个
,3个![]() ,…,n个
,…,n个![]() (n为正整数)顺次排成一列:1,
(n为正整数)顺次排成一列:1,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() ,…,记a1=1,a2=
,…,记a1=1,a2=![]() ,a3=
,a3=![]() ,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
,…,S1=a1,S2=a1+a2,S3=a1+a2+a3,…,Sn=a1+a2+…+an,则S2018=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知蜗牛从![]() 点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:
点出发,在一条数轴上来回爬行,规定:向正半轴运动记作“+”,向负半轴运动记作“-”,从开始到结束爬行的各段路程(单位:![]() )依次为:+7,-5,-10,-8,+9,-6,+12,+4.
)依次为:+7,-5,-10,-8,+9,-6,+12,+4.
(1)若![]() 点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;
点在数轴上表示的数为-3,则蜗牛停在数轴上何处,请通过计算加以说明;
(2)蜗牛在(1)题在数轴上停的位置作以下运动:第1次向左移动1个单位长度至![]() 点,第2次从
点,第2次从![]() 点向右移动2个单位长度至
点向右移动2个单位长度至![]() 点,第3次从
点,第3次从![]() 点向左移动3个单位长度至
点向左移动3个单位长度至![]() 点,第4次从
点,第4次从![]() 点向右移动4个单位长度至
点向右移动4个单位长度至![]() 点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案).
点,…,依此类推.这样第2019次移动到的点在数轴上表示的数为(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CA=CB=5,AB=6,AB⊥y轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.
(x>0)的图象经过点C,交AB于点D.
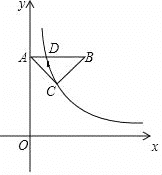
(1)若OA=8,求k的值;
(2)若CB=BD,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com