小杰从正面观察左边的热水瓶时.得到的俯视图是( ) C [解析]试题分析:从正面看下面是一个矩形.中间是一个梯形.上边是一个矩形.左边是一个矩形. 故选:A．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

小杰从正面（图示“主视方向”）观察左边的热水瓶时，得到的俯视图是（）

C 【解析】试题分析：从正面看下面是一个矩形，中间是一个梯形，上边是一个矩形，左边是一个矩形. 故选：A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：2017-2018学年山东省德州市六校七年级（上）第一次联考数学试卷 题型：单选题

已知x＝－3是方程k(x＋4)－2k－x＝5的解，则k的值是(　　)

A. －2 B. 2 C. 3 D. 5

A 【解析】试题分析：把x=-3代入k（x+4）-2k-x=5，得：k×（-3+4）-2k+3=5，解得：k=-2．故选A．

查看答案和解析>>

科目：初中数学 来源：陕西省2018届九年级上学期期中考试数学试卷 题型：解答题

（分）计算：

．

1 【解析】试题分析：按照实数的运算顺序进行运算即可. 试题解析：原式．

查看答案和解析>>

科目：初中数学 来源：人教版九年级年级数学下册第二十九章达标检测卷 题型：解答题

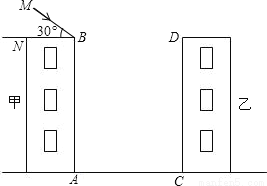
如图，两幢楼高AB=CD=30m，两楼间的距离AC=24m，当太阳光线与水平线的夹角为30°时，求甲楼投在乙楼上的影子的高度．（结果精确到0.01，≈1.732，≈1.414）

投到乙楼影子高度是16.14m 【解析】试题分析：（1）首先要作出甲楼投到乙楼的影子，如下图所示,线段CE即表示乙楼的影子；（2）求甲楼投在乙楼上的影子的高度即需求线段CE的长,为此,必须要求出DE的长，而DE为Rt△DEB的边长，且楼间距AC=BD=24m，∠DBE=30°，所以解这个直角三角形即可求解. 【解析】如图，延长MB交CD于E，连接BD，由于A...

查看答案和解析>>

科目：初中数学 来源：人教版九年级年级数学下册第二十九章达标检测卷 题型：填空题

墙壁CD上D处有一盏灯（如图），小明站在A处测得他的影长与身长相等，都为1.6m，他向墙壁走1m到B处时发现影子刚好落在A点，则灯泡与地面的距离CD=_____．

m 【解析】试题分析：利用相似三角形的相似比，列出方程组，通过解方程组求出灯泡与地面的距离即可．试题解析：如图：根据题意得：BG=AF=AE=1.6m，AB=1m， ∵BG∥AF∥CD， ∴△EAF∽△ECD，△ABG∽△ACD， ∴AE：EC=AF：CD，AB：AC=BG：CD，设BC=xm，CD=ym，则CE=（x+2.6）m，AC=（x+1）m...

查看答案和解析>>

科目：初中数学 来源：2017-2018学年黑龙江省哈尔滨市双城区七年级（上）期末数学试卷（五四学制） 题型：解答题

如图所示，OE，OD分别平分∠AOC和∠BOC，

（1）如果∠AOB=90°，∠BOC=38°，求∠DOE的度数；

（2）如果∠AOB=α，∠BOC=β（α、β均为锐角，α＞β），其他条件不变，求∠DOE；

（3）从（1）、（2）的结果中，你发现了什么规律，请写出来．

（1）45° ；（2）α；（3）∠DOE的大小与∠BOC的大小无关．【解析】试题分析：（1）首先计算出∠AOC的度数，然后再根据角平分线的性质可得∠COE=∠AOC，∠COD=∠BOC，根据∠DOE=∠COE-∠COD代入角度计算即可；（2）方法与（1）相同，首先计算出∠AOC的度数，然后再根据角平分线的性质可得∠COE=∠AOC，∠COD=∠BOC，根据∠DOE=∠COE-∠COD代...