
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED,若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.如图2,已知△ABC中,AB=AC,过边AB上的点D作DE∥BC交AC于点E,过点E作边AB的逆平行线EF,交边BC于点F.
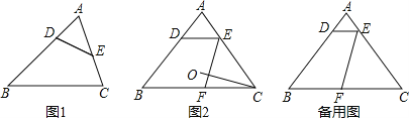
(1)求证:DE是边BC的逆平行线.
(2)点O是△ABC的外心,连接CO.求证:CO⊥FE.
(3)已知AB=5,BC=6,过点F作边AC的逆平行线FG,交边AB于点G.
①试探索AD为何值时,四边形AGFE的面积最大,并求出最大值;
②在①的条件下,比较AD+BG______AB大小关系.(“<、>或=”)
【答案】(1)见解析;(2)见解析;(3)①当AD=![]() ,四边形有最大值,最大值为
,四边形有最大值,最大值为![]() ,②=
,②=
【解析】
(1)根据题干条件可证得∠B=∠ACB,则∠BDE+∠B=180°,∠BDE+∠ACB=180°,结论得证;
(2)连接AO,证得∠FEC=∠B,由OA=OC可得∠OAC=∠OCA,∠BAO=∠OAC,证出∠FEC+∠ACB=90°,即CO⊥FE;
(3)①由题意设FC=x,则BF=6-x,证△FEC∽△ABC,可得![]() ,同理可得
,同理可得![]() ,四边形AGFE的面积可表示为S△ABC-S△EFC-S△BFG,利用二次函数的性质可求出最大值;
,四边形AGFE的面积可表示为S△ABC-S△EFC-S△BFG,利用二次函数的性质可求出最大值;
②由①知点F为BC的中点,连接DF,根据EF为AB边的逆平行线,可证得DF为AC边的逆平行线,则G点与D点重合,则AD+BG=AB.
解:(1)证明:
∵AB=AC,
∴∠B=∠ACB,
∵DE∥BC,
∴∠BDE+∠B=180°,∠BDE+∠ACB=180°,
∴DE是边BC的逆平行线.
(2)证明:如图,连接AO,
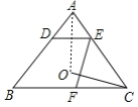
∵EF是边BA的逆平行线,
∴∠AEF+∠B=180°,
∵∠AEF+∠FEC=180°,
∴∠FEC=∠B,
∵点O是△ABC的外心,
∴OA=OC,OA平分∠BAC,
∴∠OAC=∠OCA,∠BAO=∠OAC,
∵∠BAO+∠B=90°,
∴∠FEC+∠ACB=90°,
∴CO⊥FE.
(3)①设FC=x,BF=6-x,S四边形AGFE=y,
∵∠FEC=∠B,∠FCE=∠ACB,
∴△FEC∽△ABC.
∴![]() ,
,
∴![]() ,
,
同理可得S△BFG=![]()
∴y=S△ABC-S△EFC-S△BFG=12-![]() =-
=-![]() ,
,
∴当x=3时,有AD=![]() ,此时y有最大值,最大值为
,此时y有最大值,最大值为![]() .
.
②在①的条件下CF=BF=3,如图,连接DF,
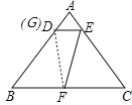
∵BF=CF,∠B=∠C,BD=CE,
∴△BDF≌△CEF(SAS),
∴∠BDF=∠CEF,∠BFD=∠EFC,
∴∠BFE=∠DFC,∠AEF=∠ADF.
∵∠AEF+∠B=180°,∠A+∠BFE=180°,
∴∠C+∠ADF=180°,∠A+∠DFC=180°.
∴FD为边AC的逆平行线,
由题意可知D与G点重合,
∴AD+BG=AB,
故答案为:=.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC,BD交于O,EO⊥AC.
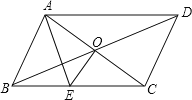
(1)若△ABE的周长为10cm,求平行四边形ABCD的周长;
(2)若∠ABC=78°,AE平分∠BAC,试求∠DAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.抛掷一枚硬币四次,有两次正面朝上B.射击运动员射击一次,命中十环
C.打开电视频道,正在播放《奔跑吧,兄弟》D.方程![]() 必有实数根
必有实数根
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在研究相似问题时,甲、乙同学的观点如下:
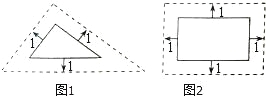
甲:将边长为3、4、5的三角形按图1的方式向外扩张,得到新三角形,它们的对应边间距为1,则新三角形与原三角形相似.
乙:将邻边为3和5的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形相似.
对于两人的观点,下列说法正确的是( )
A.甲对,乙不对 B.甲不对,乙对 C.两人都对 D.两人都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的最大公里数(单位:km/L),如图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况,下列叙述正确的是( )

A. 以相同速度行驶相同路程,甲车消耗汽油最多
B. 以10km/h的速度行驶时,消耗1升汽油,甲车最少行驶5千米
C. 以低于80km/h的速度行驶时,行驶相同路程,丙车消耗汽油最少
D. 以高于80km/h的速度行驶时,行驶相同路程,丙车比乙车省油
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2x+m-1=0.
(1)若此方程有两个不相等的实数根,求实数m的取值范围;
(2)当Rt△ABC的斜边长c=![]() ,且两直角边a和b恰好是这个方程的两个根时,求Rt△ABC的面积.
,且两直角边a和b恰好是这个方程的两个根时,求Rt△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y![]() x+3分别与x轴,y轴交于点A、点B,抛物线y=x2+2x﹣2与y轴交于点C,点E在抛物线y=x2+2x﹣2的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
x+3分别与x轴,y轴交于点A、点B,抛物线y=x2+2x﹣2与y轴交于点C,点E在抛物线y=x2+2x﹣2的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.4B.4.6C.5.2D.5.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D,AB,DC的延长线交于点E.
(1)求证:AC平分∠DAB;
(2)若BE=3,CE=3![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
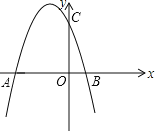
【题目】如图,抛物线y=ax2+bx+3与x轴交于A(﹣3,0),B(l,0)两点,与y轴交于点C.
(1)求抛物线的解析式;
(2)点P是抛物线上的动点,且满足S△PAO=2S△PCO,求出P点的坐标;
(3)连接BC,点E是x轴一动点,点F是抛物线上一动点,若以B、C、E、F为顶点的四边形是平行四边形时,请直接写出点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com