
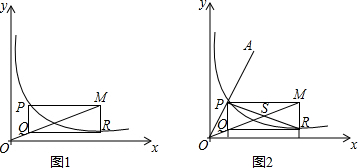
分析 (1)延长PQ交x轴于点H,设点P(a,$\frac{1}{a}$),R(b,$\frac{1}{b}$),则Q(a,$\frac{1}{b}$),M(b,$\frac{1}{a}$),再由tan∠QOH=tan∠MOB即可得出结论;
(2)根据PR=2OP,PR=2PS,得出OP=PS,∠PSO=∠POS.再由∠PSO=2∠PMO,∠PMO=∠MOB可得出结论.
解答 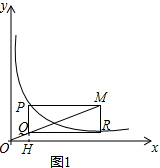 解:(1)如图1,延长PQ交x轴于点H,设点P(a,$\frac{1}{a}$),R(b,$\frac{1}{b}$),
解:(1)如图1,延长PQ交x轴于点H,设点P(a,$\frac{1}{a}$),R(b,$\frac{1}{b}$),
∵四边形PQRM是矩形,
∴Q(a,$\frac{1}{b}$),M(b,$\frac{1}{a}$).
∵tan∠QOH=$\frac{QH}{OH}$=$\frac{1}{ab}$,tan∠MOB=$\frac{MB}{OB}$=$\frac{1}{ab}$,
∴∠QOH=∠MOB,即点Q在直线OM上;
(2)如图2,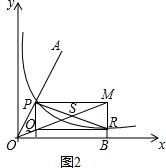
∵PR=2OP,PR=2PS,
∴OP=PS,
∴∠PSO=∠POS.
∵∠PSO=2∠PMO,∠PMO=∠MOB,
∴∠MOB=$\frac{1}{3}$∠AOB.
点评 本题考查的是反比例函数综合题,熟知反比例函数图象上点的坐标特点及矩形的性质是解答此题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
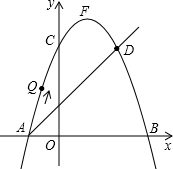 如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.
如图,在平面直角坐标系中,直线AD与抛物线y=-x2+bx+c交于A(-1,0)和D(2,3)两点,点C、F分别为该抛物线与y轴的交点和顶点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
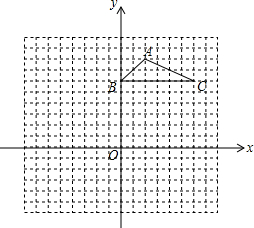 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立如图所示的平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
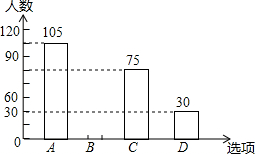 某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:
某中学在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如下两种不完整的统计图表:| 选项 | 球类运动 | 百分比 |
| A | 乒乓球 | 35% |
| B | 羽毛球 | x |
| C | 篮球 | 25% |
| D | 其他 | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
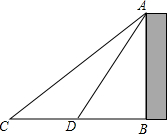 天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)
天津北宁公园内的致远塔,塔高九层,塔内四周墙壁上镶钳着历史题材为内容的瓷板油彩画或青石刻浮雕,叠双向盘旋楼梯或电梯可达九层,津门美景尽收眼底,是我国目前最高的宝塔.某校数学情趣小组实地测量了致远塔的高度AB,如图,在C处测得塔尖A的仰角为45°,再沿CB方向前进31.45m到达D处,测得塔尖A的仰角为60°,求塔高AB(精确到0.1m,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.
如图,在△ABC中,AB=AC=6,BC=4,⊙B与边AB相交于点D,与边BC相交于点E,设⊙B的半径为x.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
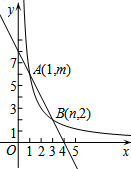 直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).
直线y=-2x+8和双曲线y=$\frac{k}{x}$(k≠0)交于点A(1,m),B(n,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
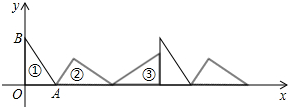 如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).
如图①,在△AOB中,∠AOB=90°,OA=3,OB=4,将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑧的直角顶点的坐标为($\frac{144}{5}$,$\frac{12}{5}$).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com