
| 2 |
| 1 |
| 2 |
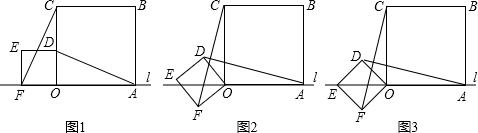
 解:(1)AD=CF.
解:(1)AD=CF.
|
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AG2+DG2 |
| 42+12 |
| 17 |
| 17 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 5 |
| 2 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•湘潭)如图,C岛位于我南海A港口北偏东60方向,距A港口60
(2013•湘潭)如图,C岛位于我南海A港口北偏东60方向,距A港口60| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•湘潭)6月5日是世界环境日,今年“世界环境日”中国的主题为“同呼吸,共奋斗”,旨在释放和传递:建设美丽中国,人人共享、人人有责的信息,小文积极学习与宣传,并从四个方面A:空气污染,B:淡水资源危机,C:土地荒漠化,D:全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项).以下是他收集数据后,绘制的不完整的统计图表:
(2013•湘潭)6月5日是世界环境日,今年“世界环境日”中国的主题为“同呼吸,共奋斗”,旨在释放和传递:建设美丽中国,人人共享、人人有责的信息,小文积极学习与宣传,并从四个方面A:空气污染,B:淡水资源危机,C:土地荒漠化,D:全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项).以下是他收集数据后,绘制的不完整的统计图表:| 关注问题 | 频数 | 频率 |
| A | 24 | 0.4 |
| B | 12 | 0.2 |
| C | n | 0.1 |
| D | 18 | m |
| 合计 | a | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com