
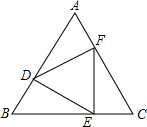 如图,在等边△ABC的三边上分别取点D、E、F,使AD=BE=CF.
如图,在等边△ABC的三边上分别取点D、E、F,使AD=BE=CF.分析 (1)由△ABC是等边三角形,AD=BE=CF,易证得△ADF≌△BED,即可得DF=DE,同理可得DF=EF,即可证得:△DEF是等边三角形;
(2)由(1)证得△ADF≌△BED,得到BD=AF,通过△ABF≌△CBD,得到∠ABF=∠BCD,求得∠RPQ=∠FBC+∠BCD=60°,同理∠PQR=∠PRQ=60°,于是得到结论.
解答 证明:(1)∵△ABC是等边三角形,
∴AB=BC=AC,
∵AD=BE=CF,
∴AF=BD,
在△ADF和△BED中,$\left\{\begin{array}{l}{AD=BE}\\{∠A=∠B}\\{AF=BD}\end{array}\right.$,
∴△ADF≌△BED(SAS),
∴DF=DE,
同理DE=EF,
∴DE=DF=EF.
∴△DEF是等边三角形;
(2)△PQR是等边三角形,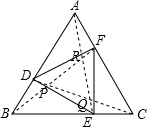
理由:由(1)证得△ADF≌△BED,
∴BD=AF,
在△ABF与△CBD中,$\left\{\begin{array}{l}{AB=BC}\\{∠BAC=∠CBD}\\{AF=BD}\end{array}\right.$,
∴△ABF≌△CBD,
∴∠ABF=∠BCD,
∵∠ABF+∠CBF=60°,
∴∠CBF+∠BCD=60°,
∵∠RPQ=∠FBC+∠BCD=60°,
同理∠PQR=∠PRQ=60°,
∴△PQR是等边三角形.
点评 此题考查了等边三角形的判定与性质,全等三角形的判定与性质,熟练掌握等边三角形的判定和性质是解题的关键.


科目:初中数学 来源: 题型:解答题
| 日 期 | 15日 | 16日 | 17日 | 18日 | 19日 | 20日 | 21日 | 22日 |
| 天然气表显示的读数/m3 | 220 | 229 | 241 | 249 | 259 | 270 | 279 | 290 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
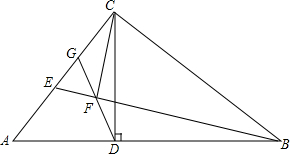 已知Rt△ABC中,∠ACB=90°,CD是高,E为AC上一点,CF⊥BE于F,FD的延长线交AC于G.
已知Rt△ABC中,∠ACB=90°,CD是高,E为AC上一点,CF⊥BE于F,FD的延长线交AC于G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
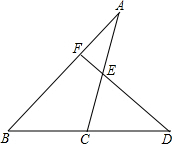 如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.
如图,已知D是△ABC边BC延长线上一点,DF⊥AB于点F,交AC于点E,∠A=35°,∠D=42°,求(1)∠ACD的度数; (2)∠AEF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由.
某地区有一种植物在气温0℃以下持续时间超过2.5小时,即遭霜冻灾害,需采取预防措施,如图是气象台某天发布的该地区气象信息,预报了次日0时至5时气温随时间变化情况,气温是时间的二次函数,它的图象经过点(0,2),其顶点坐标是($\frac{5}{2}$,-$\frac{9}{8}$),请你根据图中信息判断这种植物次日是否需要采取防冻措施?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
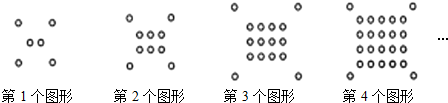
| 图形序号 | 1 | 2 | 3 | 4 | 5 |
| 小圆个数 | 6 | 10 | 16 | 24 | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com