
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.动点
的中点.动点![]() 从点
从点![]() 出发以每秒
出发以每秒![]() 个单位向终点
个单位向终点![]() 匀速运动(点
匀速运动(点![]() 不与
不与![]() 、
、![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 的垂线交折线
的垂线交折线![]() 于点
于点![]() .以
.以![]() 、
、![]() 为邻边构造矩形
为邻边构造矩形![]() .设矩形
.设矩形![]() 与
与![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() ,点
,点![]() 的运动时间为
的运动时间为![]() 秒.
秒.
(1)直接写出![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值;
的值;
(3)当矩形![]() 与
与![]() 重叠部分图形不是矩形时,求
重叠部分图形不是矩形时,求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(4)沿直线![]() 将矩形
将矩形![]() 剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的
剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合条件的![]() 的值.
的值.
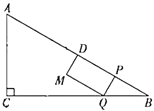
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3) ;(4)
;(4)![]() 或
或![]()
![]() .
.
【解析】
(1)根据P点的运动速度和BD的长度即可出结果;
(2)画出图象,根据三角形的相似求出各个线段长,即可解决;
(3)分情况讨论,矩形![]() 与
与![]() 重叠部分面积即为矩形面积减去△ABC外部的小三角形面积,通过三角函数计算出各边长求面积即可;
重叠部分面积即为矩形面积减去△ABC外部的小三角形面积,通过三角函数计算出各边长求面积即可;
(4)要想使被直线分割成的两部分能拼成不重叠且无缝隙的图形恰好是三角形,则需要被分割的是两个至少有一条相等边长的直角三角形,或者直线正好过正方形一条边的中点,分情况画图求解即可.
解:(1)∵![]() ,
,![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
P从B运动到点D所需时间为1s,
由题意可知![]() ,
,
![]() ;
;
(2)如图所示,

由题意得![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
由四边形![]() 是矩形可知,∠QPD=∠MDP=90°,PQ=DM,即∠APQ=∠BDM=90°,
是矩形可知,∠QPD=∠MDP=90°,PQ=DM,即∠APQ=∠BDM=90°,
∵∠B=∠B,∠BDM=∠ACB=90°,
∴△MDB∽△ACB,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]()
∵∠A=∠A,∠APQ=∠ACB=90°,
∴△APQ∽△ACB,
∴![]() ,即
,即![]() ,
,
解得![]() ;
;
(3)当![]() 时,如图,DM交BC于点F,
时,如图,DM交BC于点F,
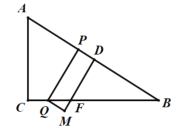
由矩形可知PD∥QM,∴∠FQM=∠B=30°,
此时![]() ,
,
∴![]() ,
,
∴![]() ,
,
解得![]() ,
,
![]() ,
,
同理![]() ,
,![]() ,解得
,解得![]() ,
,
![]() ,
,
![]() ,
,
当![]() 时,如图,DM交BC于点F,QM交BC于E,
时,如图,DM交BC于点F,QM交BC于E,

![]() ,由题意可知∠A=60°,
,由题意可知∠A=60°,
![]() ,
,
∴![]() ,即
,即![]() ,
,
![]() ,得
,得![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,
∴![]() ,
,
综上所述: ;
;
(4)如图所示,当Q与C重合时,满足条件,

由前面解题过程可知此时![]() ,
,
当PQ=DM时,此时直线CD正好过QM的中点,满足条件,

此时![]() ,
,
当直线CD正好过PQ的中点G时,满足条件,如图,

由前面计算可知![]() ,则
,则![]() ,
,
![]() ,
,
解得![]() ,
,
综上所述,![]() 或
或![]()
![]() .
.


科目:初中数学 来源: 题型:
【题目】重庆移动为了提升新型冠状肺炎“停课不停学”期间某片区网络信号,保证广大师生网络授课、听课的质量,临时在坡度为![]() 的山坡上加装了信号塔
的山坡上加装了信号塔![]() (如图所示),信号塔底端
(如图所示),信号塔底端![]() 到坡底
到坡底![]() 的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌
的距离为3.9米.同时为了提醒市民,在距离斜坡底4.4米的水平地面上立了一块警示牌![]() .当太阳光线与水平线成53°角时,测得信号塔
.当太阳光线与水平线成53°角时,测得信号塔![]() 落在警示牌上的影子
落在警示牌上的影子![]() 长为3米,则信号塔
长为3米,则信号塔![]() 的高约为(tan53°≈1.3)( ).
的高约为(tan53°≈1.3)( ).
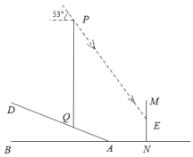
A.10.4B.11.9C.11.4D.13.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆货车从甲地出发以每小时80 km的速度匀速驶往乙地,一段时间后,一辆轿车从乙地出发沿同一条路匀速驶往甲地.货车行驶2.5 h后,在距乙地160 km处与轿车相遇.图中线段AB表示货车离乙地的距离y1 km与货车行驶时间x h的函数关系.
(1)求y1与x之间的函数表达式;
(2)若两车同时到达各自目的地,在同一坐标系中画出轿车离乙地的距离y2与x的图像,求该图像与x轴交点坐标并解释其实际意义.
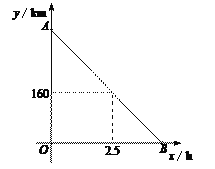
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以Rt△ABC的直角边AB为直径作半圆⊙O与边BC交于点D,过D作半圆的切线与边AC交于点E,过E作EF∥AB,与BC交于点F.若AB=20,OF=7.5,则CD的长为( )
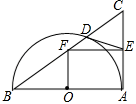
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 和抛物线
和抛物线![]() 相交于点
相交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),
的左侧),![]() 是抛物线
是抛物线![]() 上
上![]() 段的一点(点
段的一点(点![]() 不与
不与![]() 、
、![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线交抛物线
轴的垂线交抛物线![]() 于点
于点![]() ,以
,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,当正方形的四个顶点分别落在四个不同象限时,
,当正方形的四个顶点分别落在四个不同象限时,![]() 的取值范围是__________.
的取值范围是__________.
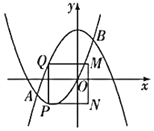
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.

(1)求证:DB平分∠ADC;
(2)若EB=10,CD=9,tan∠ABE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1,在△ABC中,∠A=75°,∠C=60°,AC=6![]() ,求△ABC的外接圆半径R的值;
,求△ABC的外接圆半径R的值;
问题探究
(2)如图2,在△ABC中,∠BAC=60°,∠C=45°,AC=8![]() ,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
,点D为边BC上的动点,连接AD以AD为直径作⊙O交边AB、AC分别于点E、F,接E、F,求EF的最小值;
问题解决
(3)如图3,在四边形ABCD中,∠BAD=90°,∠BCD=30°,AB=AD,BC+CD=12![]() ,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
,连接AC,线段AC的长是否存在最小值,若存在,求最小值:若不存在,请说明理由.
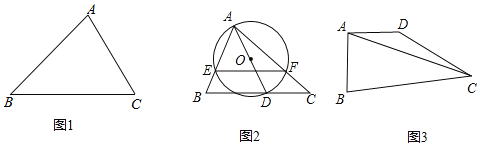
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设直线y=kx+6和直线y=(k+1)x+6(k是正整数)及x轴围成的三角形面积为Sk(k=1,2,3,…,8),则S1+S2+S3+…+S8的值是( )
A. ![]() B.
B. ![]() C. 16D. 14
C. 16D. 14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明的书包里只放了A4大小的试卷共4张,其中语文1张、数学2张、英语1张
![]() 若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
若随机地从书包中抽出2张,求抽出的试卷中有英语试卷的概率.
![]() 若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
若随机地从书包中抽出3张,抽出的试卷中有英语试卷的概率为______
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com