
【题目】如下图,已知![]() ,
,![]() ,下列条件中不能判定
,下列条件中不能判定![]() ≌
≌![]() 的是( )
的是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由平行线的性质得到两对角对应相等,若添加一对边对应相等,可得到两个三角形全等,若添加一对角相等,则不能得出三角形全等.
∵AB∥DE,∴∠B=∠DEC.
∵AC∥DF,∴∠ACB=∠F.
(1)∵BE=CF,∴BC=EF.在△ABC和△DEF中,∵∠B=∠DEC,BC=EF,∠ACB=∠F,∴△ABC≌△DEF,故A选项错误;
(2)AC=DF,则△ABC和△DEF中,∠ACB=∠F,∠B=∠DEC,AC=DF,∴△ABC≌△DEF,故B选项错误;
(3)∠A=∠D,没有边相等,无法证明△ABC≌△DEF;故C选项正确;
(4)AB=DE,则△ABC和△DEF中,∵∠B=∠DEC,∠ACB=∠F,AB=DE,∴△ABC≌△DEF,故D选项错误.
故选C.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:初中数学 来源: 题型:
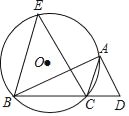
【题目】如图,点B,C为⊙O上一动点,过点B作BE∥AC,交⊙O于点E,点D为射线BC上一动点,且AC平分∠BAD,连接CE.
(1)求证:AD∥EC;
(2)连接EA,若BC=6,则当CD= 时,四边形EBCA是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD,若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A. 2![]() B. 6
B. 6![]() C. 3
C. 3![]() D.
D. ![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据要求回答下列问题:
(1)点A关于y轴对称点A′的坐标是 ;点B关于y轴对称点B′的坐标是
(2)作出△ABC关于y轴对称的图形△A′B′C′(不要求写作法)
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:营业员![]() :月销售件数100件,月总收入2400元;营业员
:月销售件数100件,月总收入2400元;营业员![]() :月销售件数150件,月总收入2700元;假设营业员的月基本工资为
:月销售件数150件,月总收入2700元;假设营业员的月基本工资为![]() 元,销售每件服装奖励
元,销售每件服装奖励![]() 元.
元.
(1)求![]() 、
、![]() 的值.
的值.
(2)若某营业员的月总收入不低于3200元,则她当月至少要卖出服装多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 和
和![]() 都是等腰三角形,
都是等腰三角形,![]() ,
,![]() ,
,![]() .
.
(初步感知)(1)特殊情形:如图①,若点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,则
上,则![]() __________
__________![]() .(填>、<或=)
.(填>、<或=)

(2)发现证明:如图②,将图①中的![]() 绕点
绕点![]() 旋转,当点
旋转,当点![]() 在
在![]() 外部,点
外部,点![]() 在
在![]() 内部时,求证:
内部时,求证:![]() .
.

(深入研究)(3)如图③,![]() 和
和![]() 都是等边三角形,点
都是等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,则
在同一条直线上,则![]() 的度数为__________;线段
的度数为__________;线段![]() ,
,![]() 之间的数量关系为__________.
之间的数量关系为__________.

(4)如图④,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,点
,点![]() 、
、![]() 、
、![]() 在同一直线上,
在同一直线上,![]() 为
为![]() 中
中![]() 边上的高,则
边上的高,则![]() 的度数为__________;线段
的度数为__________;线段![]() ,
,![]() ,
,![]() 之间的数量关系为__________.
之间的数量关系为__________.

(拓展提升)(5)如图⑤,![]() 和
和![]() 都是等腰直角三角形,
都是等腰直角三角形,![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转,连结
逆时针旋转,连结![]() 、
、![]() .当
.当![]() ,
,![]() 时,在旋转过程中,
时,在旋转过程中,![]() 与
与![]() 的面积和的最大值为__________.
的面积和的最大值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
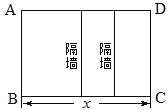
【题目】某工厂拟建一座平面图形为矩形且面积为200平方米的三级污水处理池(平面图如图ABCD所示).由于地形限制,三级污水处理池的长、宽都不能超过16米.如果池的外围墙建造单价为每米400元,中间两条隔墙建造单价为每米300元,池底建造单价为每平方米80元.(池墙的厚度忽略不计)当三级污水处理池的总造价为47200元时,求池长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 481 | 599 | 1803 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.601 | 0.599 | 0.601 |
(1)请估计:当![]() 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(白球)= .
(3)试估算盒子里黑、白两种颜色的球各有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com