
【题目】已知直线l上有三点A、B、C,且AB=6,BC=4,M、N分别是线段AB、BC的中点,则MN= .
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】随着空气质量的恶化,雾霾天气现象增多,危害加重.森林是“地球之肺”,每年能为人类提供大约28.3亿吨的有机物,28.3亿可用科学记数法表示为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
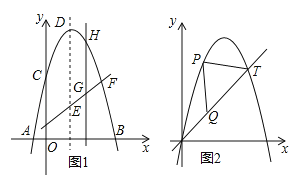
【题目】如图1所示,已知抛物线![]() 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,![]() =5:6?
=5:6?
(3)图2所示的抛物线是由![]() 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( ) 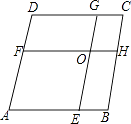
A.6.5
B.6
C.5.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中的错误的是( ).
A、一组邻边相等的矩形是正方形
B、一组邻边相等的平行四边形是菱形
C、一组对边相等且有一个角是直角的四边形是矩形
D、一组对边平行且相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用两种方法证明“三角形的外角和等于360°”.
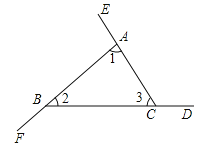
如图,∠BAE、∠CBF、∠ACD是△ABC的三个外角.
求证∠BAE+∠CBF+∠ACD=360°.
证法1:∵ ,∴∠BAE+∠1+∠CBF+∠2+∠ACD+∠3=180°×3=540°
∴∠BAE+∠CBF+∠ACD=540°﹣(∠1+∠2+∠3).
∵ ,∴∠BAE+∠CBF+∠ACD=540°﹣180°=360°.
请把证法1补充完整,并用不同的方法完成证法2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com