
【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠B=42°,∠DAE=18°.
(1)若设∠DAC=x°,则∠BAC= °,∠C= °;(用含x的代数式表示)
(2)求∠C的度数;
(3)请直接写出∠AEC与∠B、∠C之间的关系式.

【答案】(1)∠BAC=36°+2x,∠C=90°-x;(2)∠C=78°;(3)∠AEC=90°+![]() ∠B-
∠B-![]() ∠C.
∠C.
【解析】分析:(1)由角平分线的定义可得∠BAC的度数,由直角三角形两锐角互余可得到∠C的度数;
(2)由AD是BC边上的高,∠B=42°,可得∠BAD=48°,在由∠DAE=18°,可得∠BAE=∠BAD﹣∠DAE=30°,然后根据AE是∠BAC的平分线,可得∠BAC=2∠BAE=60°,最后根据三角形内角和定理即可推出∠C的度数.
(3)由三角形外角的性质和三角形内角和定理即可得出结论.
详解:(1)∵AE是∠BAC的平分线,∴∠BAC=2∠EAC=(36+2x )°.
∵AD是BC边上的高,∴∠C=90°-x.故答案为:∠BAC=36°+2x,∠C=90°-x.
(2)∵AD是BC边上的高,∠B=42°,∴∠BAD=48°.
∵∠DAE=18°,∴∠BAE=∠BAD﹣∠DAE=30°.
∵AE是∠BAC的平分线,∴∠BAC=2∠BAE=60°,∴∠C=180°﹣∠B﹣∠BAC=78°.
(3)∠AEC=∠B+∠BAE=∠B+![]() ∠BAC=∠B+
∠BAC=∠B+![]() (180°-∠B-∠C)=90°+
(180°-∠B-∠C)=90°+![]() (∠B-∠C)=90°+
(∠B-∠C)=90°+![]() ∠B-
∠B-![]() ∠C.
∠C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元,售价为每件60元,每个月可卖出200件;如果每件商品的售价每上涨1元,则每个月少卖10件.设每件商品的售价上涨x元(x为正整数),每个月的销售利润为y元.
(1)求y与x的函数关系式;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)若每个月的利润不低于2160元,售价应在什么范围?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“转化”是数学中的一种重要思想,即把陌生的问题转化成熟悉的问题,把复杂的问题转化成简单的问题,把抽象的问题转化为具体的问题.
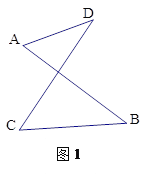
已知:如图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”,试解答下列问题:
问题一:在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系 ;
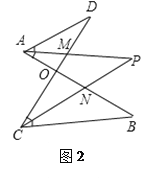
问题二:在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,试求∠P的度数;
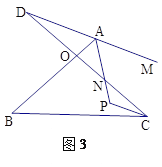
问题三:在图3中,已知AP、CP分别平分∠BAM、∠BCD,请问∠P与∠B、∠D之间存在着怎样的数量关系?并说明理由.
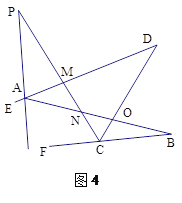
问题四:在图4中,已知AP的反向延长线平分∠EAB,CP平分∠DCF,请直接写出∠P与∠B、∠D之间的数量关系 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,![]() 的方程组
的方程组![]() ,给出下列结论:①
,给出下列结论:①![]() 是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④
是方程组的解;②无论a取何值, x,y的值都不可能互为相反数;③当a=1时,方程组的解也是方程x+y=4﹣a的解;④![]() ,
,![]() 都为自然数的解有4对.其中正确的为______________.
都为自然数的解有4对.其中正确的为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数m,若将其数字重新排列可得一个新的自然数n,如果m=3n,我们称m是一个“希望数”.例如:3105=3×1035,71253=3×23751,371250=3×123750.
(1)请说明41不是希望数,并证明任意两位数都不可能是“希望数”.
(2)一个四位“希望数”M记为![]() ,已知
,已知![]() ,且c=2,请求出这个四位“希望数”.
,且c=2,请求出这个四位“希望数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间关系的图像如图所示.根据图像解答下列问题:
(1)谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2)分别求出甲、乙两人的行驶速度;
(3)在什么时间段内,两人均行驶在途中?(不包括起点和终点)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com