
如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有
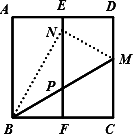
A.1个
B.2个
C.3个
D.4个
|
分析:根据题给条件,证不出①CM=DM;△BMN是由△BMC翻折得到的,故BN=BC,又点F为BC的中点,可知:sin∠BNF= 解答:解:∵△BMN是由△BMC翻折得到的, ∴BN=BC,又点F为BC的中点, 在Rt△BNF中,sin∠BNF= ∴∠BNF=30°,∠FBN=60°, ∴∠ABN=90°-∠FBN=30°,故②正确; 在Rt△BCM中,∠CBM= ∴tan∠CBM=tan30°= ∴BC= ∠NPM=∠BPF=90°-∠MBC=60°,∠NMP=90°-∠MBN=60°, ∴△PMN是等边三角形,故④正确; 由题给条件,证不出CM=DM,故①错误. 故正确的有②③④,共3个. 点评:本题考查翻折变换的知识,有一定难度,注意掌握折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等. |
|
翻折变换(折叠问题);正方形的性质. |


科目:初中数学 来源: 题型:
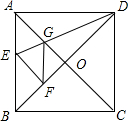 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点E,G.连接GF.下列结论:①∠AGD=112.5°;②tan∠AED=2;③S△AGD=S△OGD;④四边形AEFG是菱形;⑤BE=2OG.其中正确结论的个数是( )| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
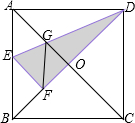 如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.
如图,在正方形纸片ABCD中,对角线AC,BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合.展开后,折痕DE分别交AB,AC于点G,E,连接GF.查看答案和解析>>
科目:初中数学 来源: 题型:
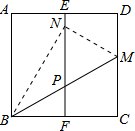 如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )
如图,在正方形纸片ABCD中,E,F分别是AD,BC的中点,沿过点B的直线折叠,使点C落在EF上,落点为N,折痕交CD边于点M,BM与EF交于点P,再展开.则下列结论中:①CM=DM;②∠ABN=30°;③AB2=3CM2;④△PMN是等边三角形.正确的有( )| A、1个 | B、2个 | C、3个 | D、4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
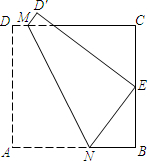 (2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则
(2013•大庆模拟)如图,在正方形纸片ABCD中,E为BC的中点.将纸片折叠,使点A与点E重合,点D落在点D′处,MN为折痕.若梯形ADMN的面积为S1,梯形BCMN的面积为S2,则| S1 |
| S2 |
| 3 |
| 5 |
| 3 |
| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
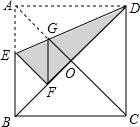 如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论:
如图,在正方形纸片ABCD中,对角线AC、BD交于点O,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,折痕DE分别交AB、AC于点E、G,连接GF.下列结论:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com