
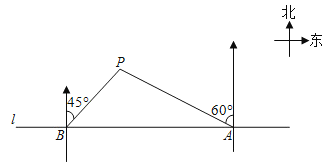
【题目】如图,在一笔直的海岸线L上有A、B两个观测点,A在B的正东方向,AB=2km.有一艘小船在点P处,从A处测得小船在北偏西60°的方向,从B处测得小船在北偏东45°方向.
(1)求P点到海岸线l的距离.
(2)小船从点P处沿射线AP的方向继续行驶,求小船到B处的最短距离.
【答案】(1)![]() ﹣1;(2)小船到B处的最短距离为1km
﹣1;(2)小船到B处的最短距离为1km
【解析】
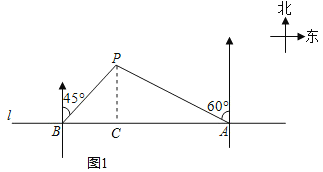
(1)作PC⊥AB于C,设PC=xkm,根据等腰直角三角形的性质、正切的定义用x表示出BC、AC,根据题意列方程求出x,得到答案;
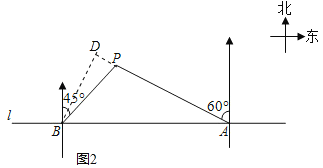
(2)作BD⊥AP交AP的延长线于D,根据直角三角形的性质解答.
解:(1)作PC⊥AB于C,
设PC=xkm,
在Rt△BCP中,∠PBC=45°,
∴BC=PC=x,
在Rt△APC中,tan∠PAC=![]() ,∠PAC=90°-60°=30°,
,∠PAC=90°-60°=30°,
∴AC=![]() =
=![]() x,
x,
由题意得,x+![]() x=2,
x=2,
解得:x=![]() ﹣1,
﹣1,
答:P点到海岸线l的距离为(![]() ﹣1)km;
﹣1)km;
(2)作BD⊥AP交AP的延长线于D,
在Rt△ADB中,∠DAB=30°,
∴BD=![]() AB=1km,
AB=1km,
答:小船到B处的最短距离为1km.


科目:初中数学 来源: 题型:
【题目】生产商对在甲、乙两地生产并销售的某产品进行研究后发现如下规律:每年年产量为![]() (吨)时所需的全部费用
(吨)时所需的全部费用![]() (万元)与
(万元)与![]() 满足关系式
满足关系式![]() ,投人市场后当年能全部售10出,且在甲、乙两地每吨的售价
,投人市场后当年能全部售10出,且在甲、乙两地每吨的售价![]() (万元)均与
(万元)均与![]() 满足一次函数关系.(注:年利润=年销售额-全部费用)
满足一次函数关系.(注:年利润=年销售额-全部费用)
(1)当在甲地生产并销售![]() 吨时,满足
吨时,满足![]() ,求在甲地生成并销售
,求在甲地生成并销售![]() 吨时利润为多少万元;
吨时利润为多少万元;
(2)当在乙地生产并销售![]() 吨时,
吨时,![]() ,求在乙地当年的最大年利润应为多少万元?
,求在乙地当年的最大年利润应为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
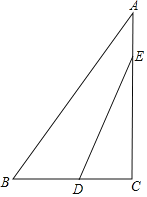
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.点E从点A出发,沿AC以每秒1个单位长度的速度向终点C运动:点D从点C出发,沿C一B一A以每秒2个单位长度的速度向终点A运动,当点E停止运动时,点D随之停止,点E、D同时出发,设点E的运动时间为t(秒)
(1)用含t的代数式表示CE的长;
(2)设点D到CA的距离为h,用含t的代数式表示h;
(3)设△CDE的面积为S(平方单位),求S(平方单位)与t(秒)的函数关系式;
(4)当DE与△ABC的边平行或垂直时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
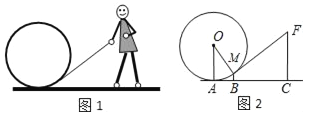
【题目】图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25 cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=![]() .
.
(1)求点M离地面AC的高度BM;
(2)设人站立点C与点A的水平距离AC=55 cm,求铁环钩MF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,OA是⊙O的半径,以OA为直径的⊙C与⊙O的弦AB相交于点D,连结OD并延长交⊙O于点E,连结AE.
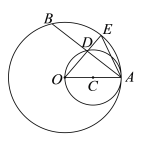
(1)求证:AD=DB.
(2)若AO=10,DE=4,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
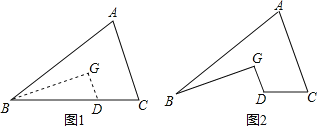
【题目】如图1,G为△ABC纸片的重心,DG∥AC交BC于点D,连结BG,剪去△BGD纸片,剩余部分纸片如图2所示,若原△ABC纸片面积为5,则图2纸片的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
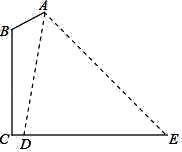
【题目】向阳中学校园内有一条林萌道叫“勤学路”,道路两边有如图所示的路灯(在铅垂面内的示意图),灯柱BC的高为10米,灯柱BC与灯杆AB的夹角为120°.路灯采用锥形灯罩,在地面上的照射区域DE的长为13.3米,从D、E两处测得路灯A的仰角分别为α和45°,且tanα=6.求灯杆AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图![]() ,若点D在
,若点D在![]() 的边AB上,且满足
的边AB上,且满足![]() ,则称满足这样条件的点为
,则称满足这样条件的点为![]() 的“理想点”
的“理想点”
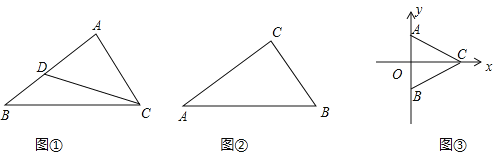
![]() 如图
如图![]() ,若点D是
,若点D是![]() 的边AB的中点,
的边AB的中点,![]() ,
,![]() ,试判断点D是不是
,试判断点D是不是![]() 的“理想点”,并说明理由;
的“理想点”,并说明理由;
![]() 如图
如图![]() ,在
,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,若点D是
,若点D是![]() 的“理想点”,求CD的长;
的“理想点”,求CD的长;
![]() 如图,已知平面直角坐标系中,点
如图,已知平面直角坐标系中,点![]() ,
,![]() ,C为x轴正半轴上一点,且满足
,C为x轴正半轴上一点,且满足![]() ,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点”
,在y轴上是否存在一点D,使点A,B,C,D中的某一点是其余三点围成的三角形的“理想点”![]() 若存在,请求出点D的坐标;若不存在,请说明理由.
若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
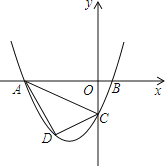
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com