
 已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标.
已知边长为2的正方形OABC在直角坐标系中(如图),OA与y轴的夹角为30°,求点A、点C、点B的坐标. 分析 由OA与y轴的夹角为30°,正方形的边长,根据三角函数值可将点A和点C的坐标直接求出,将点B的坐标设出,根据点B到点A和点O的距离,列出方程组,可将点B的坐标求出.
解答 解:过点A作AM⊥y轴于点M.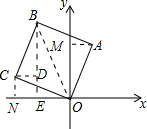
∵OA与y轴的夹角为30°,OA=OC=2,
∴AM=2×sin30°=1,OM=2×cos30°=$\sqrt{3}$,
故点A的坐标为(1,$\sqrt{3}$);
过点C作CN⊥x轴于点N.
∵OC与x轴的夹角为30°,
∴ON=2×cos30°=$\sqrt{3}$,CN=2×sin30°=1,
故点C的坐标为(-$\sqrt{3}$,1).
设点B的坐标为(a,b),
过B作BE⊥x轴,交x轴于点E,过C作CD⊥BE,交BE于点D,如图所示:
∵OB=2$\sqrt{3}$,BD=b-1,CD=$\sqrt{3}$+a,
∴$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=(2\sqrt{2})^{2}}\\{(a+\sqrt{3})^{2}+(b-1)^{2}={2}^{2}}\end{array}\right.$,
解得:b=$\sqrt{3}$+1(舍负值),a=1-$\sqrt{3}$,
∴点B的坐标为(1-$\sqrt{3}$,1+$\sqrt{3}$)
∴A(1,$\sqrt{3}$)、B(1-$\sqrt{3}$,1+$\sqrt{3}$)、C(-$\sqrt{3}$,1).
点评 本题主要是根据三角函数值将点A和点C的值求出,在根据两点之间的距离,列出方程组可将点B的坐标求出.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
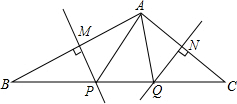 如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.
如图,在△ABC的边AB和AC的垂直平分线分别交BC于P、Q,若∠BAC=100°,则∠PAQ=20;若∠BAC+∠PAQ=150°,则∠PAQ=40°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解“嫦娥三号”卫星零部件的状况 | |
| B. | 了解在校大学生的主要娱乐方式 | |
| C. | 日光灯管厂要检测一批灯管的使用寿命 | |
| D. | 了解某市居民对废电池的处理情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
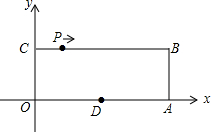 如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.
如图,平面直角坐标系xOy中,点O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在边BC上以每秒1个单位长的速度由点C向点B运动.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com