
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,且关于x的一元二次方程ax2+bx+c﹣m=0没有实数根,则下列结论:①b2﹣4ac>0;②ac<0;③m>2,其中正确结论的个数是( )

A.0B.1C.2D.3
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】“校园安全”受到社会的广泛关注,某校政教处对部分学生就校园安全知识的了解程度,进行了随机抽样调查,并绘制了如下两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有______名;
(2)请补全折线统计图,并求出扇形统计图中“基本了解”部分所对应扇形的圆心角的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
对于两个正数a、b,则![]() (当且仅当a=b时取等号).
(当且仅当a=b时取等号).
当![]() 为定值时,
为定值时,![]() 有最小值;当
有最小值;当![]() 为定值时,
为定值时,![]() 有最大值.
有最大值.
例如:已知![]() ,若
,若![]() ,求
,求![]() 的最小值.
的最小值.
解:由![]() ≥
≥![]() ,得
,得![]() ≥
≥![]() ,当且仅当
,当且仅当![]() 即
即![]() 时,
时,![]() 有最小值,最小值为
有最小值,最小值为![]() .
.
根据上面的阅读材料回答下列问题:
(1)已知![]() ,若
,若![]() ,则当
,则当![]() 时,
时,![]() 有最小值,最小值为 ;
有最小值,最小值为 ;
(2)已知![]() ,若
,若![]() ,则
,则![]() 取何值时,
取何值时,![]() 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)用长为![]() 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料:对数的创始人是苏格兰数学家纳皮尔(J.Napier,1550年-1617年),纳皮尔发明对数是在指数概念建立之前,直到18世纪瑞士数学家欧拉(Euler,1707年-1783年)才发现指数与对数之间的联系.对数的定义:一般地,若![]() ,则
,则![]() 叫做以
叫做以![]() 为底
为底![]() 的对数,记作
的对数,记作![]() .比如指数式
.比如指数式![]() 可以转化为
可以转化为![]() ,对数式
,对数式![]() 可以转化为
可以转化为![]() .我们根据对数的定义可得到对数的一个性质:
.我们根据对数的定义可得到对数的一个性质:![]()
![]() .理由如下:设
.理由如下:设![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,所以
,所以![]() ,由对数的定义得
,由对数的定义得![]() ,又因为
,又因为![]() ,所以
,所以![]() .解决以下问题:
.解决以下问题:
(1)将指数![]() 转化为对数式: .
转化为对数式: .
(2)仿照上面的材料,试证明:![]()
(3)拓展运用:计算![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学要为学校科技活动小组提供实验器材,计划购买A型、B型两种型号的放大镜,若购买8个A型放大镜和5个B型放大镜需用440元;若购买4个A型放大镜和6个B型放大镜需用304元.
(1)求每个A型放大镜和每个B型放大镜各多少元?
(2)该中学决定购买A型和B型放大镜共75个,总费用不超过2360元,则最多可以购买多少个A型放大镜?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的顶点A、C在平面直角坐标系的坐标轴上,AB=4,CB=3,点D与点A关于y轴对称,点E、F分别是线段DA、AC上的动点(点E不与A、D重合),且∠CEF=∠ACB,若△EFC为等腰三角形,则点E的坐标为______.
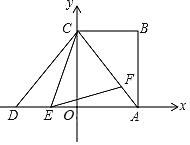
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是七年级二班参加社团活动人数的扇形统计图(每位同学只参加其中一个社团).根据统计图提供的信息,下列结论正确的是( )
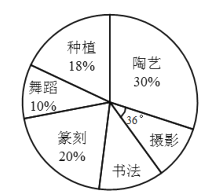
A. 参加摄影社的人数占总人数的![]()
B. 参加篆刻社的扇形的圆心角度数是![]()
C. 参加种植社的同学比参加舞蹈社的多![]() 人
人
D. 若参加书法社的人数是![]() 人,则该班有
人,则该班有![]() 人
人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师将1个黑球和若干个白球放入一个不透明的口袋并搅匀,让学生进行摸球试验,每次摸出一个球(放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.21 | 0.30 | 0.26 | 0.253 |
|
(1)![]() = ,根据上表数据估计从袋中摸出一个黑球的概率是 .
= ,根据上表数据估计从袋中摸出一个黑球的概率是 .
(2)估算袋中白球的个数为 .
(3)在(2)的条件下,若小强同学从袋中摸出两个球,用画树状图或列表的方法计算摸出的两个球都是白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com