
【题目】用配方法将关于![]() 的方程
的方程![]() 可以变形为
可以变形为![]() ,那么用配方法也可以将关于
,那么用配方法也可以将关于![]() 的方程
的方程![]() 变形为下列形式( )
变形为下列形式( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
把关于x的方程x2+5x+n=0常数项n移项后,应该在左右两边同时加上一次项系数5的一半的平方可以求得n、p的值,然后用同样的方法对关于x的方程x2-5x+n=-1进行变形.
把方程x2+5x+n=0的常数项移到等号的右边,得到x2+5x=n,
方程两边同时加上一次项系数一半的平方,得到x2+5x+(![]() )2=n+(
)2=n+(![]() )2,
)2,
配方得(x+![]() )2=n+(
)2=n+(![]() )2,
)2,
所以,根据题意,得
p=![]() ,n+(
,n+(![]() )2=9,则n=
)2=9,则n=![]() .
.
所以,由方程x25x+n=1得到
x25x![]() =1
=1
把常数项移到等号的右边,得到x25x=1+![]() ,
,
方程两边同时加上一次项系数一半的平方,得到x25x+(![]() )2=1+
)2=1+![]() +(
+(![]() )2
)2
配方得(x![]() )2=8.即(xp)2=8
)2=8.即(xp)2=8
故答案选B.


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,F为EC的中点,连接AF.写出AF与BD的数量关系和位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师提出这样一个问题:“已知![]() ,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
,同学们只用一块三角板可以画出它的角平分线吗?”聪明的小阳经过思考设计了如下方案(如图):
(1)在角的两边OM、ON上分别取OA=OB;
(2)过点A作DA⊥OM于点A,交ON于点D;过点B作EB⊥ON于点B,交OM于点E,AD、BE交于点C;
(3)作射线OC.
小阳接着解释说:“此时,△OAC≌△OBC,所以射线OC为∠MON的平分线。”小阳的方案中,△OAC≌△OBC的依据是( )

A.SASB.ASAC.HLD.AAS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,∠ACB=30°,AC=10,CD是角平分线.
(1)如图1,若E是AC边上的一个定点,在CD上找一点P,使PA+PE的值最小;
(2)如图2,若E是AC边上的一个动点,在CD上找一点P,使PA+PE的值最小,并直接写出其最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=3,M为边BC上的点,连接AM.如果将△ABM沿直线AM翻折后,点B恰好落在边AC的中点处,那么点M到AC的距离是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,
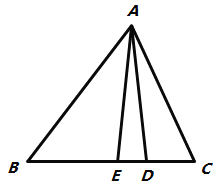
(1)若AE平分∠BAC,AD⊥BC于点D,∠C=74°,∠B=46°,求∠DAE的度数.
(2)若AE是△ABC的中线,BC=4,△ABE的面积为4,EC=3DE,求△ABC面积和△ADE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用同样规格的规格黑白两色正方形瓷砖铺设矩形地面,请观察图形并解答有关问题.

![]() 在第
在第![]() 个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含
个图中,每一横行共有________块瓷砖,每竖行共有________块瓷砖(均用含![]() 的代数式表示)
的代数式表示)
![]() 设铺设地面所用的瓷砖总块数
设铺设地面所用的瓷砖总块数![]() ,写出
,写出![]() 与
与![]() 的函数关系式(不写
的函数关系式(不写![]() 的取值范围)
的取值范围)
![]() 按上述铺设方案,铺一块这样的地面共用了
按上述铺设方案,铺一块这样的地面共用了![]() 块瓷砖,求此时
块瓷砖,求此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在长方形![]() 中,
中,![]() =4,
=4, ![]() =8,点
=8,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,则下列结论:①
,则下列结论:① ![]() ;②当
;②当![]() 时,
时,![]() 平分
平分 ![]() ; ③△
; ③△![]() 周长的最小值为15 ;④当
周长的最小值为15 ;④当![]() 时,
时,![]() 平分
平分![]() .其中正确的个数有( )
.其中正确的个数有( )

A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀平均分成4个小长方形,然后按图2的形状拼成一个正方形.

(1)图2中阴影部分的面积请用两种方法表示:① ;②_________.
(2)观察图2,请你写出式子(m+n)2,(m-n)2,mn之间的等量关系: ;
(3)若x+y=-6,xy=2.75,求x-y的值.
(4)观察图3,你能得到怎样的代数恒等式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com