
【题目】已知:如图,AB∥CD,∠1=∠2,∠3=∠4.
(1)求证:AD∥BE;
(2)若∠B=∠3=2∠2,求∠D的度数.

【答案】(1)证明见解析;(2)72°.
【解析】
根据平行线的性质推出∠1=∠ACD,求出∠2=∠ACD,根据∠2+∠CAF=∠ACD+∠CAF推出∠DAC=∠4,求出∠DAC=∠3,根据平行线的判定得出即可.根据平行线性质可求得∠D=∠DCE.
(1)证明:∵AB∥CD,
∴∠1=∠ACD,
∵∠BCD=∠4+∠E,
∵∠3=∠4,
∴∠1=∠E,
∵∠1=∠2,
∴∠2=∠E,
∴AD∥BE;
(2)解:∵∠B=∠3=2∠2,∠1=∠2,
∴∠B=∠3=2∠1,
∵∠B+∠3+∠1=180°,
即2∠1+2∠1+∠1=180°,解得∠1=36°,
∴∠B=2∠1=72°,
∵AB∥CD,
∴∠DCE=∠B=72°,
∵AD∥BE,
∴∠D=∠DCE=72°.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】平面内有三点A(2,2![]() ),B(5,2
),B(5,2![]() ),C(5,
),C(5,![]() )
)
(1)请确定一个点D,使四边形ABCD为长方形,写出点D的坐.
(2)求这个四边形的面积(精确到0.01).
(3)将这个四边形向右平移2个单位,再向下平移![]() 个单位,求平移后四个顶点的坐标.
个单位,求平移后四个顶点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4, ![]() ),B(﹣1,2)是一次函数y=kx+b与反比例函数
),B(﹣1,2)是一次函数y=kx+b与反比例函数 ![]() (m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.
(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D. 
(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?
(2)求一次函数解析式及m的值;
(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,过边AB上一点N作AB的垂线交BC于点M.
(1)如图1,若∠A=40°,求∠NMB的度数.
(2)如图2,若∠A=70°,求∠NMB的度数.
(3)你可以再分别给出几个∠A(∠A为锐角)的度数,你发现规律了吗?写出当∠A为锐角时,你猜想出的规律,并进行证明.
(4)当∠A为直角、钝角时,是否还有(3)中的结论(直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业1~5月份利润的变化情况图所示,以下说法与图中反映的信息相符的是( )
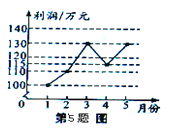
A. 1~2月份利润的增长快于2~3月份分利润的增长
B. 1~4月份利润的极差与1~5月份利润的极差不同
C. 1~5月份利润的的众数是130万元
D. 1~5月份利润的中位数为120万元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,AD和过点C的切线互相垂直,垂足为D,直线DC与AB的延长线相交于P.弦CE平分∠ACB,交直径AB于点F,连结BE. 
(1)求证:AC平分∠DAB;
(2)探究线段PC,PF之间的大小关系,并加以证明;
(3)若tan∠CEB= ![]() ,BE=5
,BE=5 ![]() ,求AC、BC的长.
,求AC、BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
∵![]() <
<![]() <
<![]() ,即2<
,即2<![]() <3,
<3,
∴1<![]() <2.
<2.
∴![]() ﹣1的整数部分为1.
﹣1的整数部分为1.
∴![]() ﹣1的小数部分为
﹣1的小数部分为![]() ﹣2
﹣2
(解决问题)![]() 的小数部分是多少;
的小数部分是多少;
我们还可以用以下方法求一个无理数的近似值.
阅读理解:求![]() 的近似值.
的近似值.
解:设![]() =10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
=10+x,其中0<x<1,则107=(10+x)2,即107=100+20x+x2.
因为0<x<1,所以0<x2<1,所以107≈100+20x,解之得x≈0.35,即![]() 的近似值为10.35.
的近似值为10.35.
理解应用:利用上面的方法求![]() 的近似值(结果精确到0.01).
的近似值(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
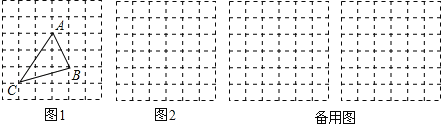
【题目】在△ABC中,AB、BC、AC三边的长分别为![]() ,
, ![]() ,
, ![]() ,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.小明同学在解答这道题时,先画一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)△ABC的面积为 .
(2)若△DEF的三边DE、EF、DF长分别为![]() ,
, ![]() ,
, ![]() ,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
,请在图2的正方形网格中画出相应的△DEF,并求出△DEF的面积为 .
(3)在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
,AC=4,BC=2,以AB为边向△ABC外作△ABD(D与C在AB异侧),使△ABD为等腰直角三角形,则线段CD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com